Planar Point Location

Sarnak and Tarjan's Persistent Search Trees

The worst case scenario for slabs results form the requirement to store separate search structures, such as a binary search tree, for each slab. This space requirement may be reduced using the fact that the set of line segments intersecting contiguous slabs are very similar. This is particularly true of the worst case example given in the previous section.

Considering the x-coordinate for each vertex to be time, and looking at how the set of line segments change as time changes from negative to positive infinity gives rise to a new search structure with reduced storage requirements. As we pass from one slab to its neighbour some segments are inserted, while others are deleted, but for the most part the search structure stays the same. Over the entire range of the subdivision there are 2n such insertions and deletions. Thus the heart of such a point location then becomes the problem of storing a sorted set, subject to insertions and deletions, that will allow efficient access to both the current information but also past versions of the structure. Such a search structure is called persistent as opposed to ephemeral structures such as a standard binary search tree, where once the structure is changed there is no way of accessing the earlier version of the structure.

Sarnak and Tarjan's solution to the planar point location problem was to develop a persistent binary search tree with O(log m), access, insertion, and deletion time, and an amortized storage requirement of O(1) per update, where m is the number of updates. Overall the structure results in an O(n) space requirement and O(log n) query time for point queries.

A persistent search structure may be developed by starting with an ephemeral search tree and transforming it into a persistent one using path copying. Sarnak and Tarjan used a red-black tree though other tree structures would also be suitable. When the tree is modified, rather than make a new copy of the tree, which will produce the O(n²) storage requirement noted earlier for slab partitioning, only the nodes in which the changes are made are copied to the new tree. Any node containing a pointer to a copied node is itself copied. Since a node has two child pointers copying a node requires copying the entire path from the altered node to the root of the tree, and thus the term path copying. This technique creates a set of search trees, 1 per update, having differing roots but sharing common sub-trees. For red black trees the node colourings may be overwritten without impacting queries for any time. Finally, an array of the tree roots, ordered by creation time, is stored. Assuming that update times are integer values roots may be accessed in constant time or in O(log m) time should we remove the integer value assumption.

Copying the entire path during during a single update can lead to non-linear storage which is sub-optimal. A possible work around is to allow nodes to become arbitrarily fat so that when a pointer is changed the new pointer is stored, along with a time stamp and a flag indicating the direction of the pointer. Thus each insertion or deletion creates only a single new node on only O(1) pointer changes. However this introduces a new time penalty as searching now must scan through all times stored at a node to select the appropriate child pointers. The time penalty is eliminated using limited node copying. Each node is permitted to hold k pointers in addition to the original two, where k is a small positive constant (k = 1 was used in the original paper). When a pointer is added to a node if there is an empty slot the pointer is simply added to the node. If there is no empty slot the node is copied setting the initial left and right pointers to their latest values such that the new node now has k empty slots and a pointer is stored to the copy in the latest parent of the copied node. If the parent has no free slot it too is copied and so on up the tree until the root is copied or we come to a free slot.

Searching in this data structure involves examining the left and right pointers to determine which direction to search and examining the time stamp to select among possibly multiple left or right pointers. The original left or right child is searched if the node has no additional pointers, or, if such additional pointers are present, the pointer with the latest time stamp not greater than the current time is followed. Fig. 1 provides a demonstration of this search structure.

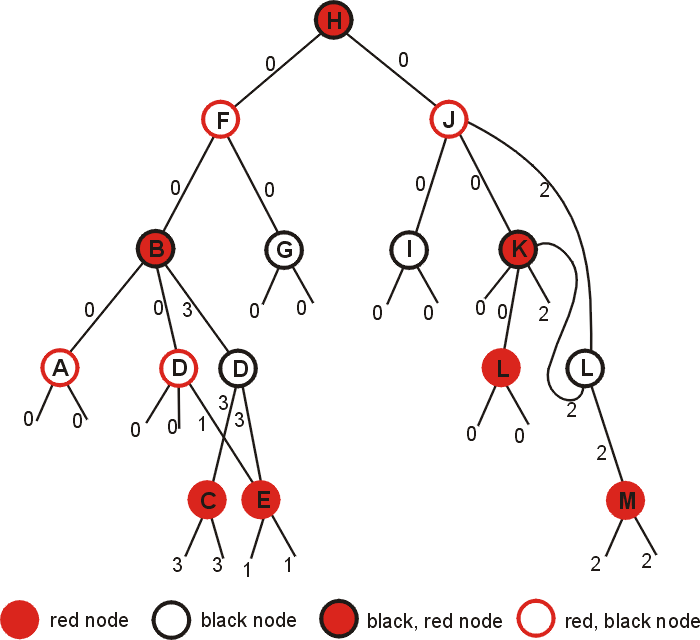
Fig 1: A persistent Red-Black tree with limited node copying and k=1. The initial tree, existing at time 0 contains items A, B, D, F, G, H, I J, K. Item E is inserted at time 1, item M at time 2, and item C at time 3. Since node colour may change this has been indicated with the node border indicating the colour at time 3 and the node interior indicating the initial node colour. Pointers are labeled by their time of creation. Figure based on Sarnak and Tarjan (1986).