Planar Point Location

Trapezoid Maps

First we will consider a few requirements for a trapezoidal map before describing structure itself. The edges of any planar subdivision are non-crossing when their only interesection, if any, occurs at a common endpoint. Given a subdivision of non-crossing edges a bounding rectangle, R may be placed around the subdivision so that the search region is bounded. Finally, assume that no two vertices in the subdivision have the same x-coordinate. This assumption is strong, and will often be violated in real world datasets, however for discussion purposes we will consider that this condition can be met, and indeed this problem can be worked around, but the presentation of the topic is more straightforward given this assumption. A set of line segments meeting the three requirements just listed, being non-crossing, having a bounding region, and with no two vertices having the same x-coordinate are termed line segments in general position.

The trapezoidal map T(S) of a set of lines in general position is generated by drawing two vertical extensions from each endpoint, p in S, one upward and one downward until they meet either a segment in S or R. A planar subdivision and its resulting trapezoid map are shown below in figure 1. Each face in the trapezoid map is bounded by one or two vertical sides and exactly two non-vertical sides, such that each face forms a triangle or trapezoid and thus the structures name.

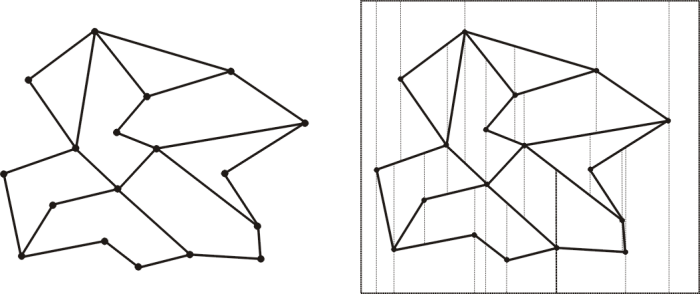
Fig. 1: A planar subdivision and its resulting trapezoid map (based on de Berg (2000)).

An individual trapezoid t, or face consists of three or four sides. The vertical side of a trapezoid may be formed by either a vertical side, or a segment endpoint. Any face may be defined by four elements, a left endpoint leftp(t) and right endpoint rightp(t) a segment above the trapezoid top(t) and a segment below the trapezoid bottom(t). A trapezoid may have one or two vertical lines depending on whether leftp(t) or rightp(t) is the common endpoint of the top(t) and bottom(t) segments. There are ten possible trapezoid configurations, three of which are shown in Figure 2. The other configurations can be derived from these three simply by changing the side that the common endpoint falls on to rightp(t), having the segment defining the rightp(t) and leftp(t) switch between top(t) and bottom(t), and finally through various combinations of having the vertical edges defined by abutting segments (the leftmost image) and by endpoints on the top(t) and bottom(t). Trapezoids are considered adjacent when they meet along a vertical edge, while sharing a common line segment, top(t) or bottom(t) produces no explicit association. When trapezoids border on a common vertical segment then this segment will be either a top(t) or a bottom(t) segment for both, this allows us to define a set of relations between adjacent trapezoids. For the trapezoid t its up to four neighbours are defined as:

1. A upper left neighbour, sharing the vertical edge defined by leftp(t) and the segment defined by top(t)
2. A upper right neighbour, sharing the vertical edge defined by rightp(t) and the segment defined by top(t)
3. A lower left neighbour, sharing the vertical edge defined by leftp(t) and the segment defined by bottom(t)
4. A lower right neighbour, sharing the vertical edge defined by rightp(t) and the segment defined by bottom(t)

Note that a trapezoid may have a few as two neighbours when its defining leftp(t) and rightp(t) are on the top(t) and bottom(t) segments, and may even have only one when leftp(t) or rightp(t) is the common endpoint of its top(t) and bottom(t) segments.

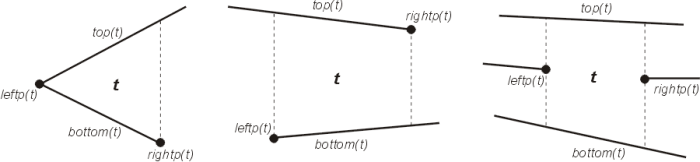
Fig. 2: Possible trapezoid configurations (based on de Berg (2000)).