Discrete Mathematics Study Center

Algorithms

An algorithm is a finite set of precise instructions for solving a problem.

Here is an algorithm for outputting the largest number from a list of $n$ numbers. Such a number is called a maximum.

set a temporary variable to the first number
compare the next number to the temporary variable
- if it is larger, set the temporary variable to this number
repeat step 2 until there are no more numbers left
return the value of the temporary variable

Here is an algorithm for outputting the index of the number $x$ from an array of $n$ numbers. This is called a linear search.

look at the first element
- if it is equal to $x$, then return that index
look at the next element
- if it is equal to $x$, then return that index
repeat step 2 until the end of the array is reached
return not found

Sorting

For the sorting problem, we are given a list of elements that can be ordered (typically numbers) and wish to rearrange the list so that the elements are in non-decreasing order.

One algorithm that solves this problem is BubbleSort. It works by looking at pairs of elements in the list and "swapping" them whenever they are out of order. If this is done enough times, then the list will be in order! In pseudocode:

			BubbleSort$\left(a_1, a_2, \ldots, a_n\right)$
				for $i \gets 1$ to $n-1$
					for $j \gets 1$ to $n-i$
						if $a_j > a_{j+1}$
							swap $a_j$ and $a_{j+1}$
						end if
					end for
				end for

Here is how the BubbleSort algorithm works on the array $3,2,4,1,5$:

\begin{array}{c@{\hskip 0.5in}c@{\hskip 0.5in}c@{\hskip 0.5in}c} i=1 & i=2 & i=3 & i=4 \\\hline \underbrace{3,2}_\text{swap},4,1,5 & \underbrace{2,3}_\text{good},1,4,|5 & \underbrace{2,1}_\text{swap},3,|4,5 & \underbrace{1,2}_\text{good},|3,4,5 \\ 2,\underbrace{3,4}_\text{good},1,5 & 2,\underbrace{3,1}_\text{swap},4,|5 & 1,\underbrace{2,3}_\text{good},|4,5 \\ 2,3,\underbrace{4,1}_\text{swap},5 & 2,1,\underbrace{3,4}_\text{good},|5 & & \\ 2,3,1,\underbrace{4,5}_\text{good} & & & \\ \end{array}

A natural question to ask is, "How long does this take?" The answer is: it depends! (On operating system, hardware, implementation, and many other things)

Another algorithm for sorting is InsertionSort.

it works by scanning the array left to right, looking for an element that is out of order
when such an element is found, it looks for where the element should go and places it there
- first, it must make room for the element, so it pushes the elements between where it was and where it should go back one

In pseudocode:

			InsertionSort$\left(a_1,a_2,\ldots,a_n\right)$
				for $j \gets 2$ to $n$
					$k \gets a_j$
					$i \gets j-1$
					while $i > 0$ and $a_i > k$
						$a_{i+1} \gets a_i$
						$i \gets i-1$
					end while
					$a_i \gets k$
				end for

Here is how the InsertionSort algorithm works on the array $3,2,4,1,5$:

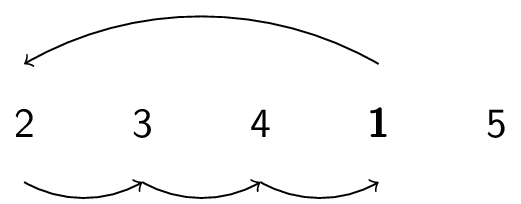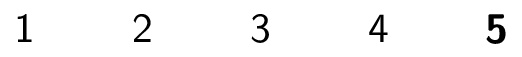How long does this take? Again, it depends. But how does it compare to BubbleSort? (Assuming same hardware, operating system, etc.)

Analysis of Algorithms

To determine how "long" an algorithm takes, we need to know how long operations (such as additions, comparisons, etc.) take. To do this, we define a model of computation.

There are many such models. For now, let's say that comparisons (\ie, $\lt,\le,\gt,\ge,=,\neq$) take one time unit ("unit time"). The actual amount of time varies (with hardware, etc.), but we assume they all take the same time. This is generally a fair assumption.

The number of such operations is the time complexity of an algorithm. Typically, we will be interested in worst-case time complexity: the maximum number of operations performed.

Here are some examples of deriving time complexity:

Recall the algorithm to find the maximum number among a list of numbers. Here is the associated pseudocode:
```
						Maximum$\left(a_1,a_2,\ldots,a_n\right)$
							max $\gets a_1$
							for $i \gets 2$ to $n$
								if $a_i >$ max
									max $\gets a_i$
								end if
							end for
							return max
					
```
We use one comparison in each iteration of the for-loop (to ensure $i \le n$) and one comparison inside the for-loop to check if $a_i > $max. Since there are $n-1$ iterations, we do $2(n-1)$ comparisons. Note that one additional comparison is needed to exit the loop (the comparison for which $i \le n$ is false), so the total is therefore $2(n-1)+1 = 2n-1$ comparisons.

In this case, the worst case is the same as any case, since we always perform each of these comparisons regardless of the input.
What about linear search? Here is the associated pseudocode:
```
						LinearSearch$\left(x,a_1,a_2,\ldots,a_n\right)$
							for $i \gets 1$ to $n$
								if $a_i = x$
									return $i$
								end if
							end for
							return not found
					
```
As before, there is one comparison in each iteration of the loop, and then one comparison inside the loop. In the worst case, we have to perform every iteration of the loop (we do not find the element and return "early"), for a total of $2(n-1)+1 = 2n-1$ comparisons, just as in the last example.

Nevertheless, we could be "lucky" and find that $x=a_1$ after performing just $2$ comparisons. Generally, we are more interested in the worst case than the best case.
What about BubbleSort?
```
						BubbleSort$\left(a_1, a_2, \ldots, a_n\right)$
							for $i \gets 1$ to $n-1$
								for $j \gets 1$ to $n-i$
									if $a_j > a_{j+1}$
										swap $a_j$ and $a_{j+1}$
									end if
								end for
							end for
					
```
The outer loop goes through $n-1$ iterations and the inner loop goes through $n-i+1$ iterations. Each inner iteration does one comparison to check the loop condition and one comparison to check if $a_j > a_{j+1}$. One additional comparison is needed to leave the inner loop, and one additional comparison is needed to leave the outer loop. The total is therefore:
\begin{array}{rcl} && \displaystyle\sum_{i=1}^{n-1} \left( 1 + \left(\sum_{j=1}^{n-i} 2\right) + 1\right) + 1 \\ &=& \displaystyle\sum_{i=1}^{n-1} \left( 2(n-i-1+1) + 2\right) + 1 \\ &=& \displaystyle\sum_{i=1}^{n-1} (2n-2i + 2) + 1 \\ &=& \displaystyle 2n\sum_{i=1}^{n-1} 1 - 2\sum_{i=1}^{n-1} i + 2\sum_{i=1}^{n-1} 1 + 1 \\ &=& 2n(n-1) - 2\frac{n(n-1)}{2} + 2(n-1) + 1 \\ &=& n(n-1) + 2n - 2 + 1\\ &=& n^2 - n + 2n -2 + 1\\ &=& n^2 + n - 1\\ \end{array}
Notice that this is always the same because there is no opportunity to be "lucky" and return early.
What about InsertionSort?
```
					InsertionSort$\left(a_1,a_2,\ldots,a_n\right)$
						for $j \gets 2$ to $n$
							$k \gets a_j$
							$i \gets j-1$
							while $i > 0$ and $a_i > k$
								$a_{i+1} \gets a_i$
								$i \gets i-1$
							end while
							$a_i \gets k$
						end for
					
```
We use one comparison per iteration of the outer loop (plus one to exit). The worst-case for the inner loop is that $i$ gets decremented from $j-1$ all the way to $0$, for a total of $j-1$ iterations with two comparisons each, plus two to exit. The total number of comparisons is therefore:
\begin{array}{rcl} && \displaystyle\sum_{j=2}^n \left(1 + \left(\sum_{i=1}^{j-1} 2\right) +2 \right) + 1\\ &=& \displaystyle \sum_{j=2}^n \left(1 + 2(j-1) + 2\right) + 1\\ &=& \displaystyle \sum_{j=2}^n \left(1 + 2j - 2 + 2\right) + 1\\ &=& \displaystyle \sum_{j=2}^n \left(2j+1\right) + 1\\ &=& \displaystyle \sum_{j=2}^n \left(2j\right) + \sum_{j=2}^n \left(1\right) + 1\\ &=& \displaystyle 2\sum_{j=2}^n j + (n-2+1) + 1\\ &=& \displaystyle 2\left(\frac{n(n+1)}{2} -1\right) + n - 2\\ &=& \displaystyle n(n+1) - 2 + n - 2\\ &=& \displaystyle n^2 + n - 2 + n - 2\\ &=& \displaystyle n^2 + 2n - 4\\ \end{array}
Notice that this could be less if we are "lucky" and fewer iterations of the while-loop are required!

Notice that BubbleSort uses $n^2 + n - 1$ comparisons while InsertionSort uses $n^2 + 2n - 4$ comparisons. Therefore, BubbleSort uses fewer comparisons in the worst case.

But are these two functions really that different? Both have a $n^2$ term, which is much bigger than any (constant) fraction that they are multiplied by, and much bigger than any linear function of $n$ they are added to. As $n$ grows bigger and bigger, the $n^2$ part makes the biggest difference. In the worst case, these functions behave approximately the same.

Contrast this with finding the maximum and linear search: both use $2n-1$ comparisons. This is much faster than the two sorting algorithms, even though the leading term has coefficient $2$. This is because $n$ grows much more slowly than $n^2$. We care about large $n$.

Therefore, for the analysis of algorithms, we don't care too much about the exact function (since it is often too much work to find!) What matters is how fast the function grows.