Countable and Uncountable Sets
Notice that a bijection exists between two sets if and only if they have the same size. This allows us to reason about the sizes of infinite sets.
Consider $\mathbb{Z}^+ = \{1,2,\ldots\}$. We call a set countable if:
- it is finite, or
-
it has the same cardinality as $\mathbb{Z}^+$
- i.e., there is a bijection between it and $\mathbb{Z}^+$
- i.e., the elements of the set can be listed in order (first, second, third, ...)
Otherwise, the set is uncountable.
Here are some examples.
-
Are there more positive integers or positive odd integers?
This is the same as asking if the positive odd integers are countable, which is the same thing as asking if there is a bijection from $\mathbb{Z}^+$ to $\{1,3,5,7,9,\ldots\}$.
We claim $f(n)=2n-1$ is such a bijection. To see that $f$ is injective, suppose $f(n)=f(m)$; then $2n-1=2m-1$, so $2n=2m$, so $n=m$. To see that $f$ is surjective, suppose $t \in \{1,3,5,7,9,\ldots\}$; then $t=2k-1$, so $t=2k-1=f(k)$.
Since $f$ is injective and surjective, it is bijective. Therefore, there are equally many positive integers as positive odd integers!
-
Are there more positive integers or positive rational numbers?
We need $f : \mathbb{Z}^+ \rightarrow \mathbb{Q}^+$. Note that we just need to list the positive rational numbers in some way, since the first element can be $f(1)$, the second can be $f(2)$, and so on. How do we achieve such a listing?
A rational number has the form $p/q$. Since we are dealing with positive rational numbers, we have $p,q \in \mathbb{Z}^+$. The list consists of all positive rationals with $p+q=2$, then all positive rationals with $p+q=3$, then all positive rationals with $p+q=4$, and so on. We do not repeat a number if we encounter it again. Note that there are only a finite number of rationals with $p+q=k$ for a fixed $k$! The list looks like this:
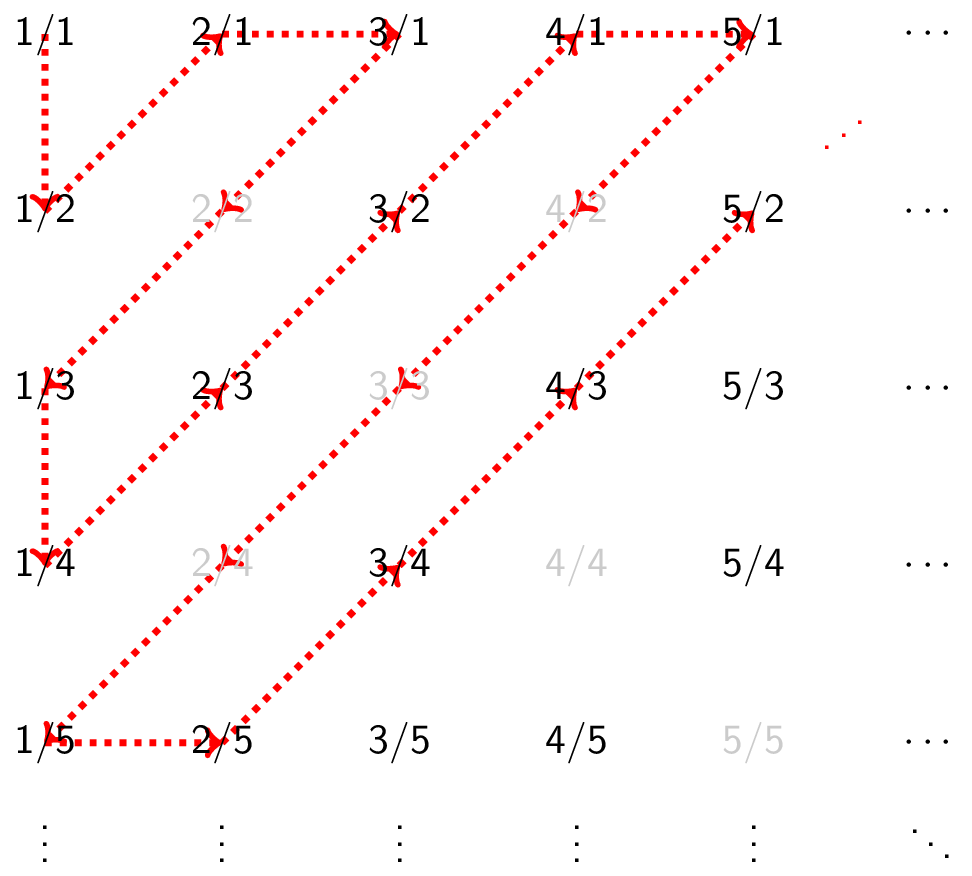
Therefore, there are equally many positive integers as positive rationals!
-
Are there more positive integers or real numbers?
This is the same as asking if $\mathbb{R}$ is countable. We will focus on an even "easier" problem: is the set $\{ x \;|\; (x \in \mathbb{R}) \land (0 \lt x \lt 1) \}$ (the set of real numbers strictly between $0$ and $1$) countable?
We will show that it is not countable. We prove this by contradiction, so suppose that it is countable. We can therefore list the elements:
- $0.d_{11}d_{12}d_{13}d_{14}\cdots$
- $0.d_{21}d_{22}d_{23}d_{24}\cdots$
- $0.d_{31}d_{32}d_{33}d_{34}\cdots$
- $0.d_{41}d_{42}d_{43}d_{44}\cdots$
- ...
Where $d_{ij} \in \{0,1,\ldots,9\}$.
Now, we come up with a real number $0 \lt x \lt 1$ that is not on this list. This will contradict the countability assumption! Consider $r = 0.d_1d_2d_3\cdots$, where $$ d_i = \begin{cases} 4 & \text{if } d_{ii} \neq 4\\ 5 & \text{if } d_{ii} = 4\\ \end{cases} $$
Notice that:
- $r \neq r_1$, since they differ in $d_1$ and $d_{11}$
- $r \neq r_2$, since they differ in $d_2$ and $d_{22}$
- $r \neq r_3$, since they differ in $d_3$ and $d_{33}$
- $\cdots$
Therefore, $r$ is not on the list, and we have a contradiction! Therefore, the real numbers are uncountable: they are bigger than $\mathbb{Z}^+$. (Why doesn't this argument work for the previous examples which were countable?)