Functions
Suppose we want to map one set to the other: given an element of set $A$ (the input), return an element of set $B$ (the output).
For example, suppose $A = \{ x \;|\; x \text{ is a user on our computer system} \}$ and $B = \{ x \;|\; x \text{ is a valid password}\}$. We might want to know, given a user, what is that user's password: the input is the user (from $A$) and the output is that user's password (from $B$).
Let $A$ and $B$ be two sets. A function from $A$ to $B$ is an assignment of exactly one element from $B$ to each element of $A$. We write $f(a) = b$ if $b \in B$ is the unique element assigned by the function $f$ to the element $a \in A$. If $f$ is a function from $A$ to $B$, we write $f : A \rightarrow B$.
It makes sense to model the password example above as a function because each user has exactly one password. Here are two other examples:
-
Suppose user root has password $\text{123}$, john has password $\text{p455w0rd}$, and guest has password $\text{hello}$. Call the password function $p$. Then $p(\texttt{root}) = \text{123}, p(\texttt{john}) = \text{p455w0rd}, p(\texttt{guest}) = \text{hello}$. We can also visualize $p$ as follows:
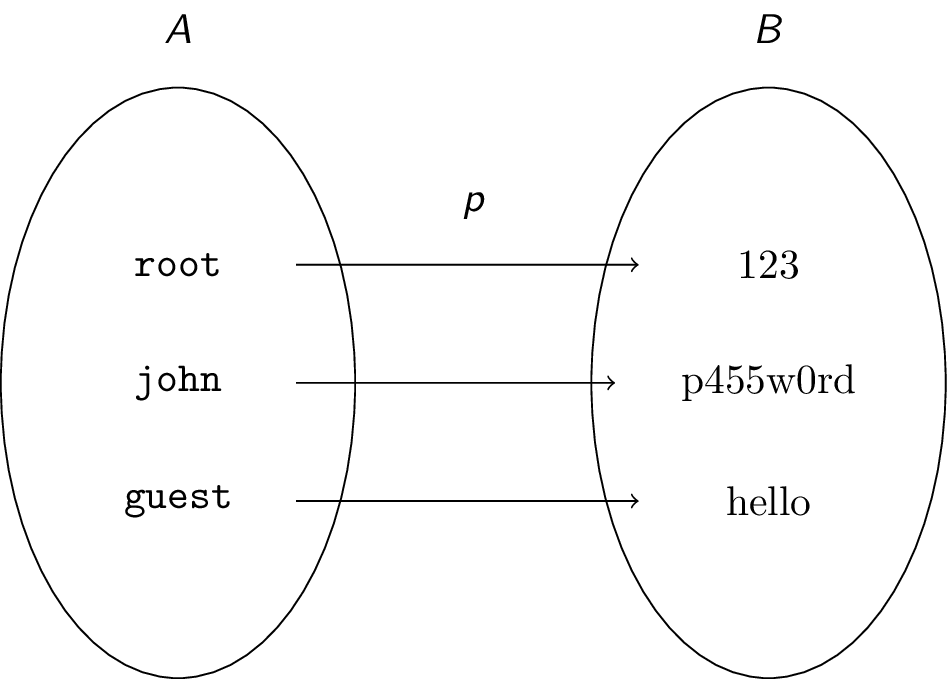
-
Consider a function $g$ that assigns a grade to each student in the class:
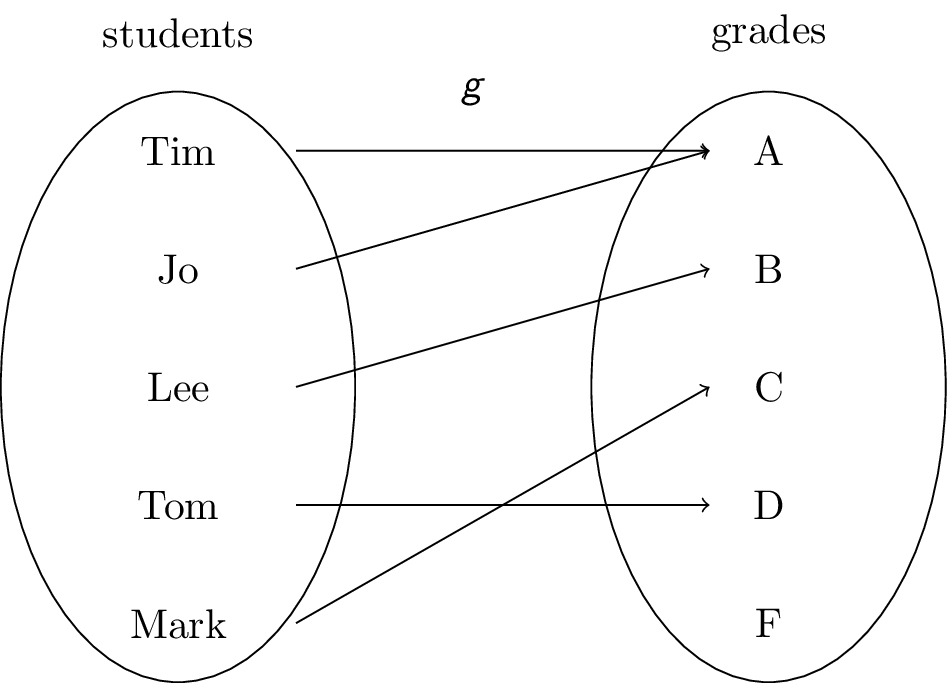
Functions can be specified in several ways:
- writing out each pair explicitly: $p(\texttt{root}) = \text{123}, \ldots$
- a diagram, as in the last two examples
- a formula: $f(x) = 2x^2 + 1$
Consider the function $f:A \rightarrow B$. We call $A$ the domain of $f$ and $B$ the codomain of $f$. Furthermore, if $f(a)=b$, then $b$ is the image of $a$ and $a$ is the preimage of $b$. The set of all images of elements of $A$ is called the range of $f$. For example:
-
In the grades example above:
- domain: $\{ \text{Tim}, \text{Jo}, \text{Lee}, \text{Tom}, \text{Mark} \}$
- codomain: $\{ \text{A}, \text{B}, \text{C}, \text{D}, \text{F} \}$
- range: $\{ \text{A}, \text{B}, \text{C}, \text{D} \}$
- $\text{A}$ is the image of $\text{Tim}$
- $\text{Tim}$ is a preimage of $\text{A}$
-
Let $f:\mathbb{Z} \rightarrow \mathbb{Z}$ be defined by $f(x)=x^2$.
- domain: $\mathbb{Z}$
- codomain: $\mathbb{Z}$
- range: $\{ x \;|\; x \text{ is a non-negative perfect square} \}$
If $S$ is a subset of the domain, we can also look at its image: the subset of $B$ that consists of the images of the elements in $S$: $f(S) = \{ f(s) \;|\; s \in S \}$. In the grades example above, $g(\{\text{Tim},\text{Jo},\text{Lee}\}) = \{\text{A},\text{B}\}$.