Notice that in the grades example, $\text{A}$ had two elements map to it, while $\text{F}$ had none. We can classify functions based on such situations.
Injectivity
A function $f$ is said to be injective or one-to-one if $(f(x) = f(y)) \rightarrow (x = y)$ for all $x$ and $y$ in the domain of $f$. The function is said to be an injection.
Recall that, by contraposition, $(f(x) = f(y)) \rightarrow (x=y)$ if and only if $(x \neq y) \rightarrow (f(x) \neq f(y))$.
Basically, this means that each element of the range has exactly one pre-image. Equivalently, each element of the codomain has at most one pre-image. In a function diagram, this means there is at most one incoming arrow to every element on the right hand side.
To show a function is injective:
- assume $f(x) = f(y)$ and show that $x=y$, or
- assume $x \neq y$ and show that $f(x) \neq f(y)$
To show a function is not injective, give an $x$ and $y$ such that $x \neq y$ but $f(x) = f(y)$.
Here are some examples:
-
The function on the left is injective, but the function on the right is not:
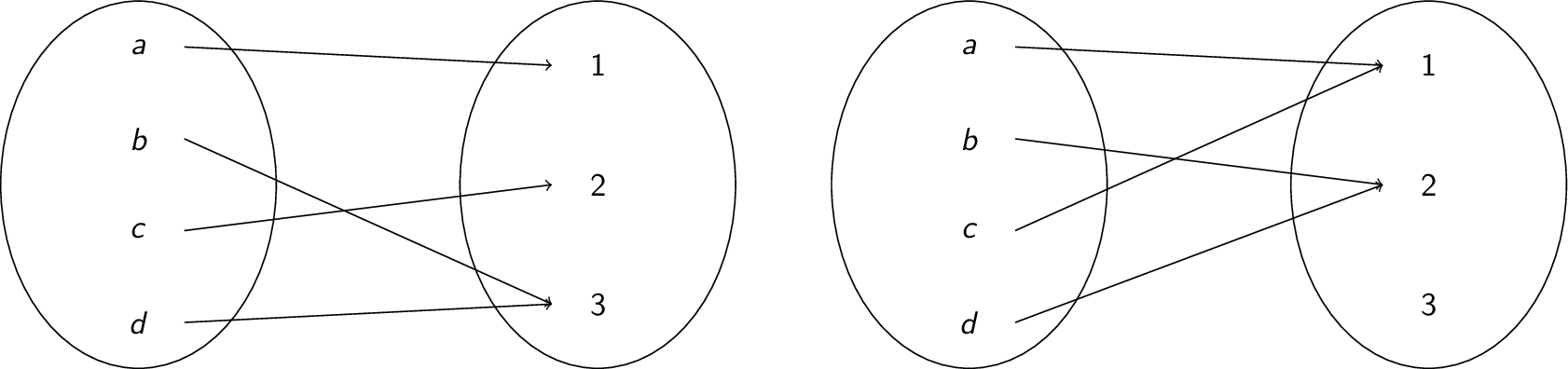
- $f : \mathbb{Z} \rightarrow \mathbb{Z}$ defined by $f(x) = 3x+2$ is injective. To see this, assume $f(x) = f(y)$. Then: \begin{array}{rcl} 3x + 2 & = & 3y + 2 \\ 3x & = & 3y \\ x & = & y \end{array}
- The previous proof falls apart for $f(x) = x^2$: \begin{array}{rcl} x^2 & = & y^2 \\ \sqrt{x^2} & = & \sqrt{y^2} \\ \pm x & = & \pm y \end{array} which is not the same thing as $x = y$! Indeed, $f(x) = x^2$ is not injective since $f(1) = 1 = f(-1)$ and $1 \neq -1$.
Surjectivity
A function $f : A \rightarrow B$ is said to be surjective or onto if for every element $b \in B$, there is an element $a \in A$ such that $f(a) = b$. The function is said to be a surjection.
Basically, this means that every element of the codomain has a pre-image. Equivalently, the codomain and range are the same. In a function diagram, this means there is at least one incoming arrow to every element on the right hand side.
To show a function is surjective, start with an arbitrary element $b \in B$ and show what the preimage of $b$ could be: show an $a \in A$ such that $f(a) = b$. To show a function is not surjective, give a $b$ such that $f(a) \neq b$ for any $a \in A$.
Here are some examples:-
The function on the left is surjective, but the function on the right is not:
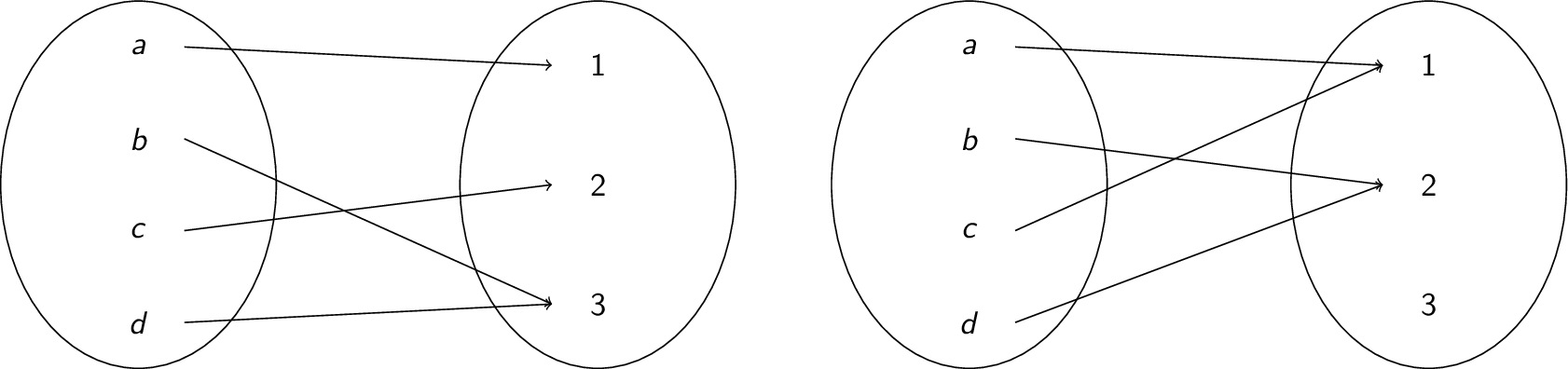
- $f : \mathbb{Z} \rightarrow \mathbb{Z}$ defined by $f(x) = x^2$ is not surjective, since there is no $x$ such that $x^2 = -1$ where $x$ is an integer.
- $f : \mathbb{R} \rightarrow \mathbb{R}$ defined by $f(x) = 3x+2$ is surjective. To see this, suppose we have image $3x+2=y$. To determine which pre-image gives this, observe that $3x+2 = y$ is the same as $3x = y-2$, which is the same as $x = (y-2)/3$. So, to get an output of $y$, give input $(y-2)/3$.
Notice that:
- injective $\leftrightarrow$ at most one image
- surjective $\leftrightarrow$ at least one image
If a function is both injective and surjective, then each element of the domain is mapped to a unique element of the codomain (range). A function that is both injective and surjective is bijective. Such a function is called a bijection.
To show a function is bijective, show:
- it is injective (using the above techniques)
- it is surjective (using the above techniques)
Remember to show both parts, since functions can be any combination of injective and surjective. For example, from left-to-right, the following functions are injective but not surjective, surjective but not injective, injective and surjective, and neither injective nor surjective:

Inverse of a Function
If a function $f$ is bijective, then $f$ is invertible. Its inverse is denoted $f^{-1}$ and assigns to $b \in B$ the unique element $a \in A$ such that $f(a) = b$: that is, $f^{-1}(b) = a \;\leftrightarrow\; f(a) = b$.
Inverses are not defined for functions that are not bijections.
- if $f$ is not injective, then some $b$ has two pre-images. Thus, $f^{-1}(b)$ would have more than one value and therefore $f^{-1}$ would not be a function
- if $f$ is not surjective, then some $b$ has no pre-image. Thus, $f^{-1}(b)$ would have no value and therefore $f^{-1}$ would not be a function
The inverse can be found by reversing the arrows in the diagram, or by isolating the other variable in the formula. Note that the inverse of $f : A \rightarrow B$ is $f^{-1} : B \rightarrow A$.
Here are some examples of functions and their inverses:
-
Consider the following function:
The function is injective and surjective and therefore bijective and invertible. We have $f^{-1}(1) = c, f^{-1}(2)=a, f^{-1}(3)=b$.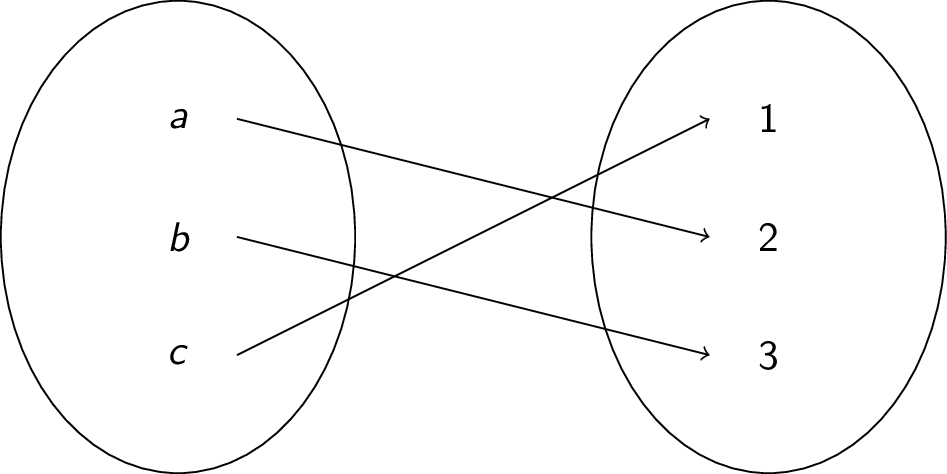
- $f : \mathbb{Z} \rightarrow \mathbb{Z}$ defined by $f(x) = 3x+2$ is bijective as we have already seen and is thus invertible. We know that $3x+2 = y \;\leftrightarrow\; 3x = y-2 \;\leftrightarrow\; x = \frac{y-2}{3}$. Therefore, $f^{-1}(x) = \frac{x-1}{3}$. (Note: it doesn't matter what variable you use, as long as you are consistent!)
- $f : \mathbb{Z} \rightarrow \mathbb{Z}$ defined by $f(x) = x^2$ is not invertible since it is not surjective.
Composition of Functions
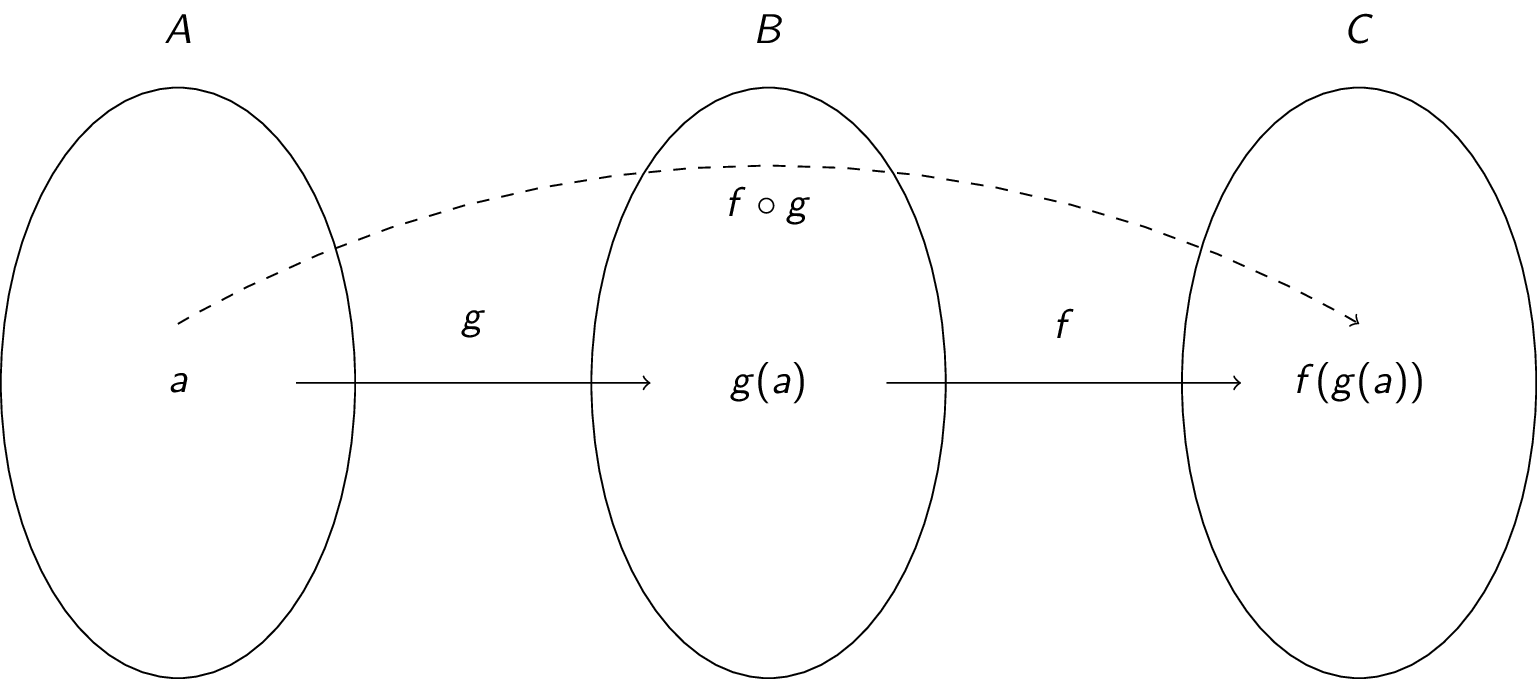
Given two functions $f$ and $g$, we can use the output of one as the input to the other to create a new function $f(g(x))$. In this function, we evaluate $g$ with input $x$ and give the result to $f$ to compute the final output.
Let $f : B \rightarrow C$ and $g : A \rightarrow B$. The composition of $f$ and $g$ is denoted $f \circ g$ (read "$f$ follows $g$") and is defined as $(f \circ g)(x) = f(g(x))$. Note: for $f \circ g$ to be defined, the range of $g$ must be a subset of the domain of $f$.
Graphically, we have:
Here are some examples:
-
Define $g : \{a,b,c\} \rightarrow \{a,b,c\}$ and $f : \{a,b,c\} \rightarrow \{1,2,3\}$ in the following way:
- $g(a) = b, g(b) = c, g(c) = a$
- $f(a) = 3, f(b) = 2, f(c) = 1$
- $(f \circ g)(a) = f(g(a)) = f(b) = 2$
- $(f \circ g)(b) = f(g(b)) = f(c) = 1$
- $(f \circ g)(c) = f(g(c)) = f(a) = 3$
- Define $f:\mathbb{Z} \rightarrow \mathbb{Z}$ and $g:\mathbb{Z} \rightarrow \mathbb{Z}$ by $f(x) = 2x+3$ and $g(x)=3x+2$. Then: \begin{array}{rcl} (f \circ g)(x) &=& f(g(x)) \\ &=& f(3x+2) \\ &=& 2(3x+2)+3 \\ &=& 6x+4+3 \\ &=& 6x+7 \\ \end{array} and \begin{array}{rcl} (g \circ f)(x) &=& g(f(x)) \\ &=& g(2x+3) \\ &=& 3(2x+3)+2 \\ &=& 6x+9+2 \\ &=& 6x+11 \\ \end{array} In general, $f \circ g \neq g \circ f$!
One important case is composing a function with its inverse: Suppose $f(a) = b$. Then $f^{-1}(b)=a$, and:
- $(f^{-1} \circ f)(a) = f^{-1}(f(a)) = f^{-1}(b) = a$
- $(f \circ f^{-1})(b) = f(f^{-1}(b)) = f(a) = b$