Graphs
Graphs can be used to model problems from virtually any field.
A graph is a pair $(V,E)$ where $V$ is a set called the vertex set and $E$ is a set called the edge set. Each edge in $E$ describes how vertices in $V$ are connected.
Here is an example of a graph:
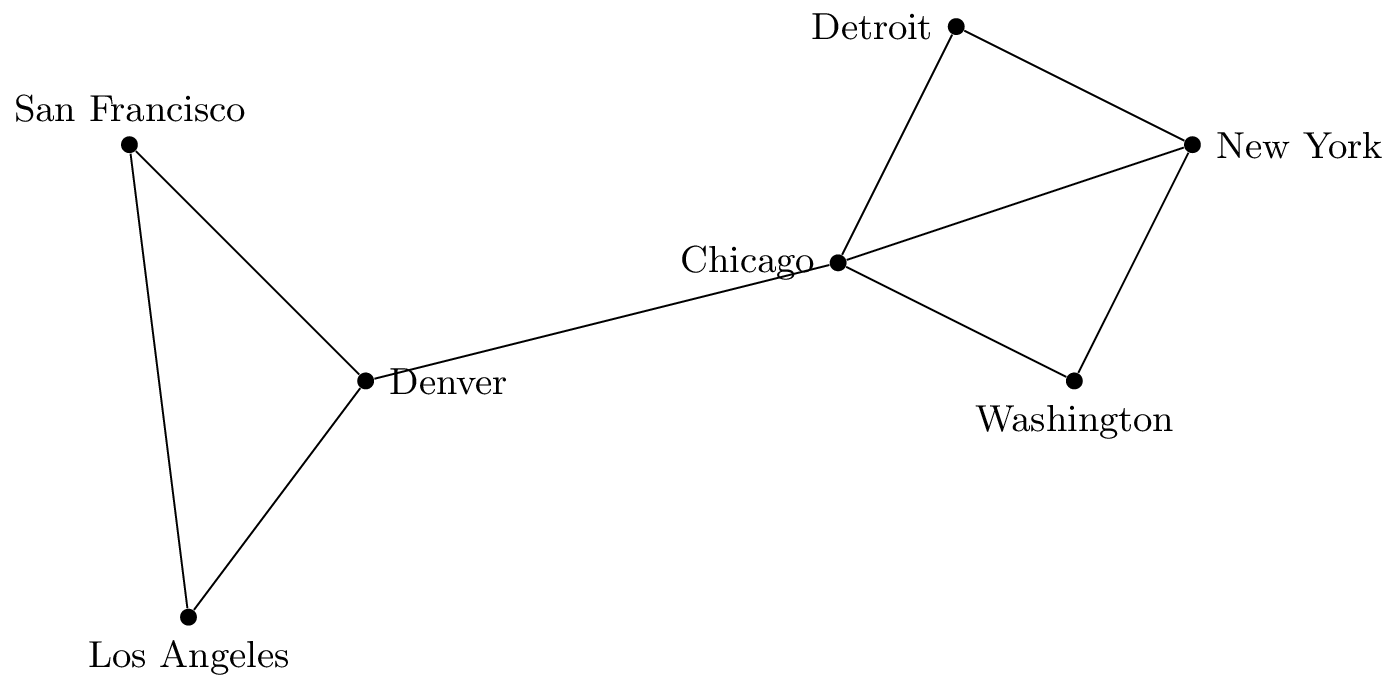
This particular graph is a simple graph:
- no edge connects a vertex to itself
- only one edge between two vertices
In this graph, edges don't have a direction. We say that the graph is undirected. Therefore, edges can be represented as sets consisting of two vertices. For the above graph,
- $V = \{ \text{San Francisco}, \text{Los Angeles}, \text{Denver}, \text{Chicago}, \text{Detroit}, \text{New York}, \text{Washington} \}$
- $E = \{\\ \,\;\{ \text{San Francisco}, \text{Denver} \},\\ \;\{ \text{San Francisco}, \text{Los Angeles} \},\\ \;\{ \text{Los Angeles}, \text{Denver} \},\\ \;\{ \text{Denver}, \text{Chicago} \},\\ \;\{ \text{Chicago}, \text{Detroit} \},\\ \;\{ \text{Detroit}, \text{New York} \},\\ \;\{ \text{New York}, \text{Washington} \},\\ \;\{ \text{Washington}, \text{Chicago} \},\\ \;\{ \text{Chicago}, \text{New York} \}\\ \}$
Sometimes, we might want to allow multiple edges between vertices. Such graphs are called multigraphs:
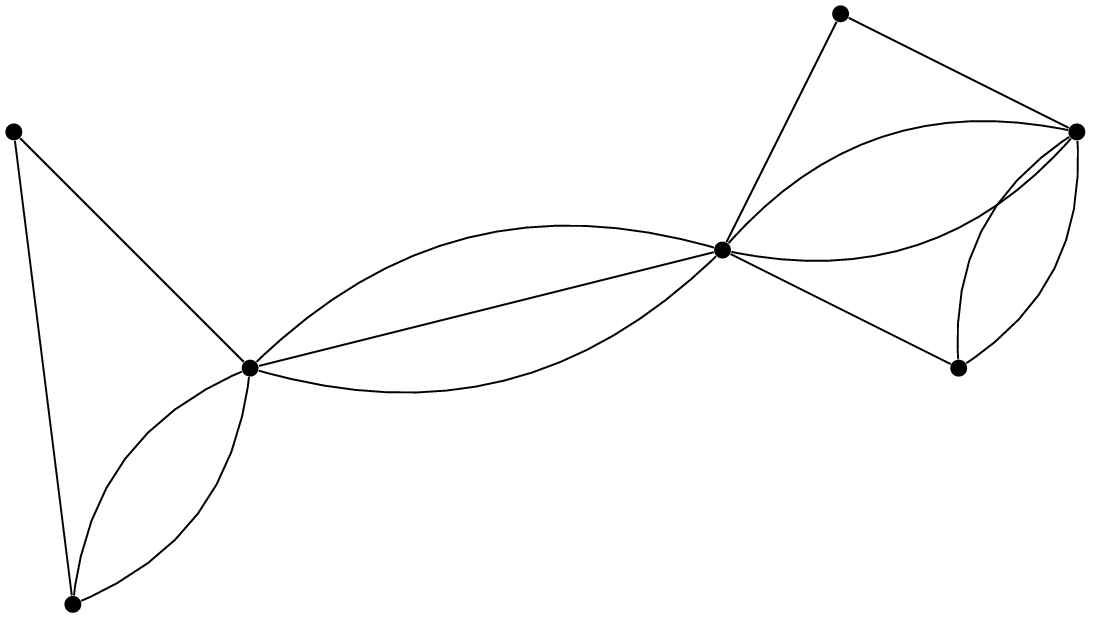
Edges are still undirected; we can represent them as sets of two vertices. However, now these sets can appear more than once. We say that if there are $m$ distinct edges between $u$ and $v$, the edge $\{u,v\}$ has multiplicity $m$. Multigraphs are used, for example, to model redundant connections in a network.
We might also want to relax the restriction that there are no edges between a vertex and itself. Such edges are called self-loops and a graph that contains self-loops is called a pseudograph. Self-loops model such things as loopbacks in networks.
We can also have directed versions of these graphs, where edges only go in one direction. Here is an example of a directed multigraph:
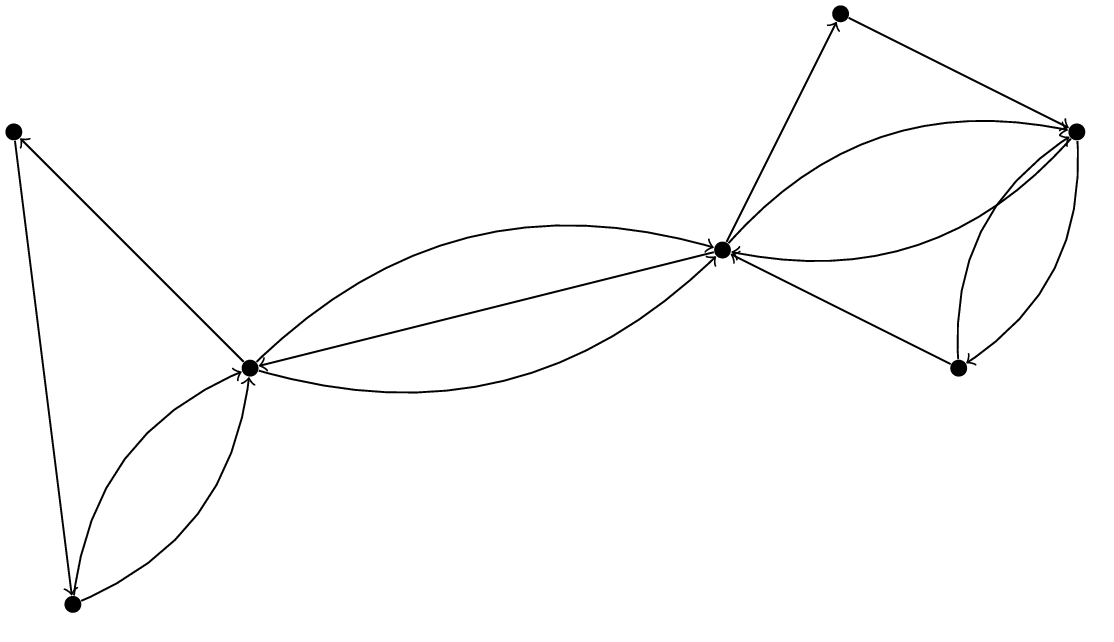
Directed edges can be represented as an ordered pair $(u,v)$ instead of a set $\{u,v\}$. Directed edges model such things as single duplex lines or one-way streets in road networks.
There are many uses of graphs:
- social networks (Facebook, etc.)
- Hollywood graph (Six Degrees of Kevin Bacon)
- Web graph
Representing Graphs
We need a way of representing graphs if we want to perform operations on them. We could simply list the vertices and edges, but that is a lot of work and it is hard to extract much information from that representation.
Here are two alternatives:
-
adjacency list: For each vertex, list the vertices that are connected to that vertex by an edge. Such vertices are said to be adjacent. (This works for both directed and undirected graphs, even if they contain loops.)
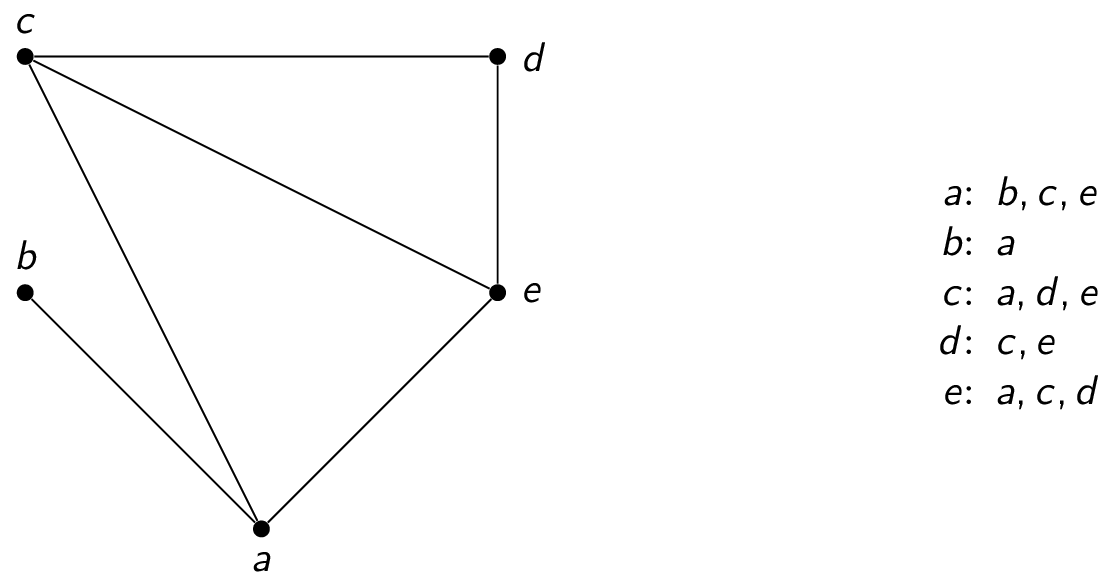
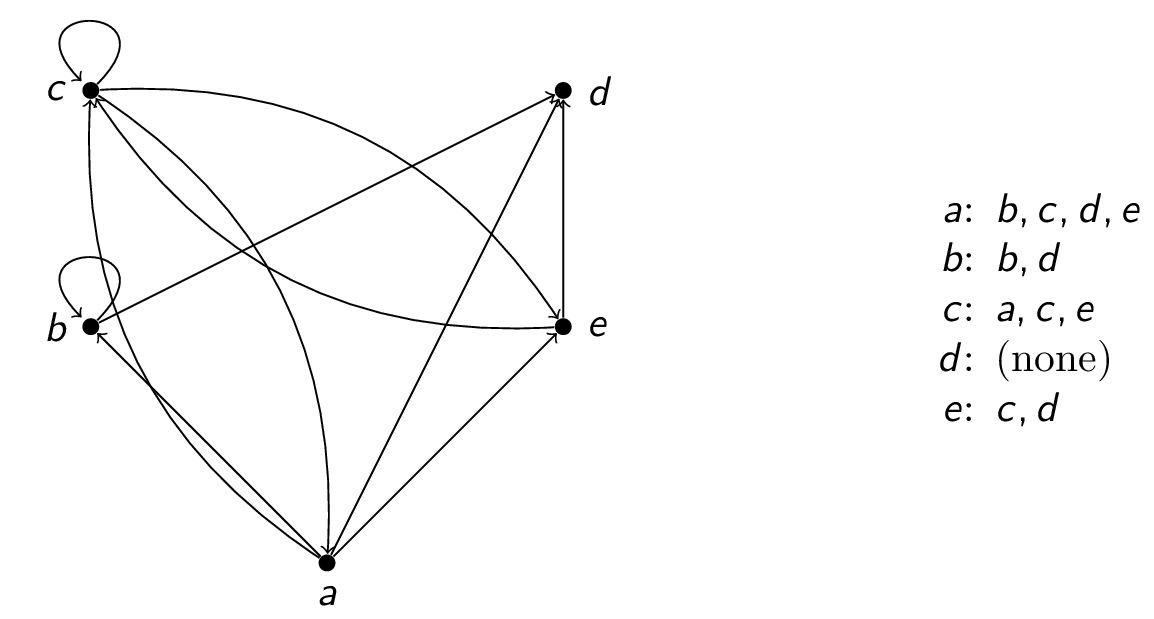
-
adjacency matrix: one row and one column for each vertex $v_1,v_2,\ldots,v_n$, row $i$ column $j$ is $1$ if the edge is in $E$, $0$ otherwise. (For this to work, you have to fix some ordering on the vertices.)
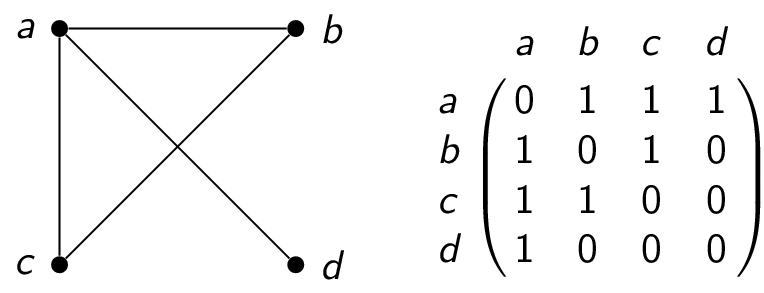
For simple undirected graphs, the adjacency matrix is symmetric ($a_{ij} = a_{ji}$ and the main diagonal is all $0$s ($a_{ii} = 0$) since no self-loops are allowed.
In general, we can allow for multigraphs by using the multiplicities as entries instead of just $0$ or $1$.

Adjacency and Degree
Let $G = (V,E)$ be a graph.
- two vertices are adjacent (are neighbours) in $G$ if $u$ and $v$ are endpoints of some edge in $G$
- if edge $e$ connects $u$ and $v$, we say $e$ is incident on $u$ (and $v$) or incident with $u$ and $v$
- the degree of a vertex in an undirected graph is the number of edges incident with it, denoted by $\deg{v}$. If a self-loop is present, it is counted twice!
For example:
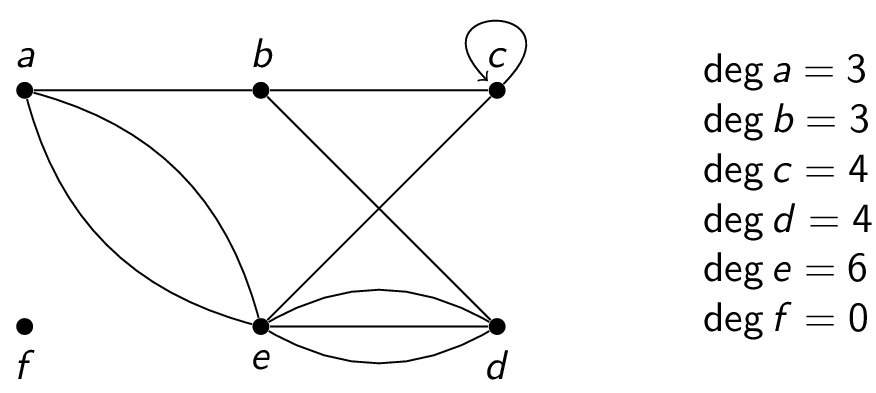
The Handshaking Theorem says that, for a graph $G=(V,E)$, we always have $$\sum_{v \in V} \deg(v) = 2|E|$$
For a directed edge $(u,v)$ in a directed graph, $u$ is the initial vertex and $v$ is the terminal vertex or end vertex.
- the number of incoming edges to $v$ (that is, the number of edges with $v$ as terminal) is denoted $\deg^-(v)$ and called the in-degree of $v$
- the number of outgoing edges from $u$ (that is, the number of edges with $u$ as initial) is denoted $\deg^+(u$ and called the out-degree of $u$
Note that $\sum_{v \in V} \deg^-(v) = \sum_{v \in V} \deg^+(v) = |E|$.
Some Special Graphs
There are a few (types of) graphs with special names:
-
the complete graph on $n$ vertices, $K_n$, has $n$ vertices, each of which is connected to all other vertices. From left to right, we have $K_1, K_2, K_3, K_4, K_5$:

-
the cycle on $n \ge 3$ vertices, $C_n$, has vertices $v_1,v_2,\ldots,v_n$ and edges $\{v_1,v_2\},\{v_2,v_3\},\ldots,\{v_{n-1},v_n\},\{v_n,v_1\}$. From left to right, we have $C_3, C_4, C_5$:

-
the wheel on $n \ge 3$ vertices, $W_n$, takes $C_n$ and adds one vertex connected to all the other vertices. From left to right, we have $W_3,W_4,W_5$:

-
a bipartite graph $G=(V,E)$ partitions $V$ into $V_1$ and $V_2$ such that $V_1 \cup V_2 = V$ and $V_1 \cap V_2 = \emptyset$, and every edge in $E$ has one endpoint in $V_1$ and one endpoint in $V_2$. This is the same as assigning one of two colours to every vertex such that no adjacent vertices have the same colour. The complete bipartite graph $K_{m,n}$ has partitions of size $m$ and $n$ and every element in one partition is connected to every element of the other partition. Here are $K_{2,3}$ and $K_{3,3}$:

Subgraphs
A subgraph of a graph $G=(V,E)$ is a graph $H=(W,F)$ such that $W \subseteq V$ and $F \subseteq E$. A subgraph $H$ of $G$ is a proper subgraph of $G$ if $H \neq G$.
For example, on the left we have $K_5$ and on the right is a subgraph of $K_5$.

A subgraph is spanning if it contains all vertices of the original graph.
Connectivity
Sometimes, we want to know if two vertices in a graph are connected by a sequence of edges that might visit other vertices on the way (for example, can two computers on a network communicate?)
A path is a sequence of edges that begins at a vertex and travels from vertex to vertex along edges of the graph.
More formally, a path of length $n \ge 0$ from vertex $u$ to vertex $v$ in $G$ is a sequence of $n$ edges $e_1,e_2,\ldots,e_n$ of $G$ such that $e_1 = \{ x_0 = u, x_1 \}, e_2 = \{ x_1,x_2 \}, \ldots, e_n = \{x_{n-1},x_n\}$.
- if the graph is simple, we can just use the vertex sequence to label the path
- the path is a circuit if $u=v$
- the path passes through vertices $x_1,x_2,\ldots,x_{n-1}$ and traverses edges $e_1,e_2,\ldots,e_n$
- a path is simple if it does not traverse an edge more than once
For example:

An undirected graph is connected if there is a path between every two distinct vertices in the graph. For example, the graph on the left is connected but the graph on the right is disconnected.

The different parts that are maximally connected are called connected components.
One special type of connected (sub)graph is a tree, which is a connected undirected graph with no simple circuits. For example, the graph on the left is a tree; the graph in the center is not a tree because it contains a circuit; and the graph on the right is not a tree because it is not connected.

Because trees are "simple" in structure, we often want to find a spanning subgraph that is a tree:
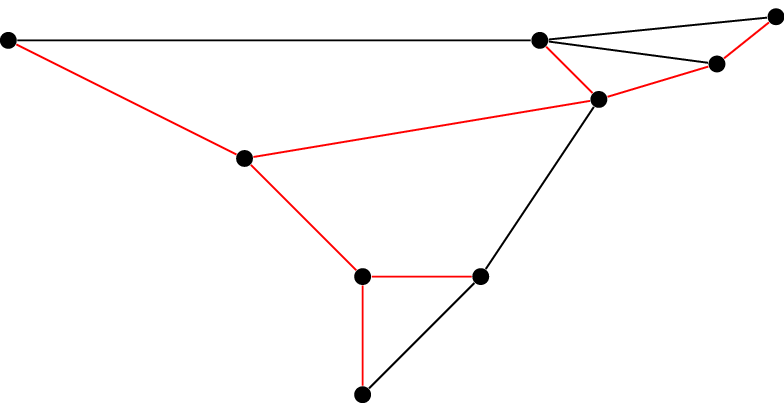
In the graph above, the red edges form a spanning subgraph because every vertex appears exactly once. It is a tree because it is connected and contains no circuits.
Returning to subgraphs in general, we note that sometimes removing a single vertex or edge would cause a graph to become disconnected:
- a cut vertex is a vertex whose removal disconnects the remaining graph (note that any edges incident on the removed vertex are removed too)
- a cut edge is an edge whose removal disconnects the remaining graph
For example, consider the following graph:
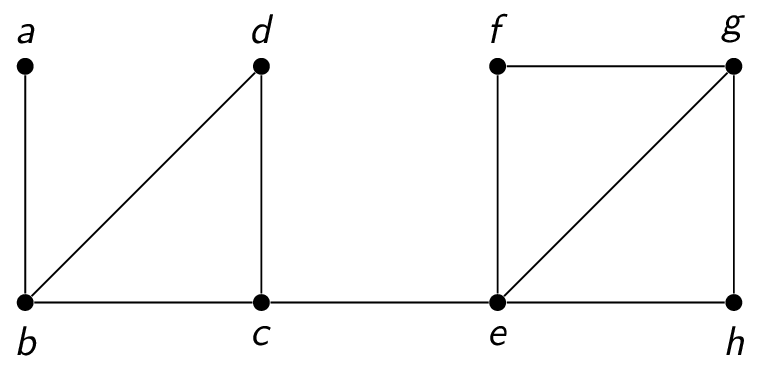
The cut vertices are $b,c,e$, and the cut edges are $\{a,b\},\{c,e\}$.
We can also talk about connectivity in directed graphs:- a directed graph is strongly connected if there is a path from $a$ to $b$ and from $b$ to $a$ for every pair of vertices $a$ and $b$
- a directed graph is weakly connected if the graph is connected when you ignore the directions of the edges (that is, the "underlying undirected graph")
For example, the graph on the left is both strongly and weakly connected, while the graph on the right is only weakly connected since there is no path from $a$ to $b$.
