Discrete Mathematics Study Center

Induction

What is the sum of the first $n$ positive odd integers?

\begin{array}{rcl} n=1: & 1 & =1 \\ n=2: & 1+3 & =4 \\ n=3: & 1+3+5 & =9 \\ n=4: & 1+3+5+7 & =16 \end{array}

So far, it seems like the pattern seems to be that the sum is $n^2$. But recognizing a pattern is not the same as a proof! How do we prove something is true for every $n$ (of which there are infinitely many)?

Imagine a long line of people, numbered $1,2,3,\ldots$. Suppose that whenever person $k$ is told something, thye tell person $k+1$. If I tell a secret to person $1$, what happens? $1$ tells $2$, $2$ tells $3$, $3$ tells $4$, and so on. So, after everyone is finished talking, everyone in the line knows what I said.

Let $P(n)$ denote the proposition "person $n$ knows the secret". The argument has premises $P(1)$ and $\forall k\;(P(k) \rightarrow P(k+1))$, with conclusion $\forall n\;P(n)$. Indeed, this is a valid argument:

\begin{array}{lll} 1. & P(1) & \\ 2. & \forall k\;(P(k) \rightarrow P(k+1)) & \therefore \forall n\;P(n) \\ \hline 3. & P(1) \rightarrow P(2) & \text{Universal Instantiation (2)} \\ 4. & P(2) & \text{Modus Ponens (1,3)} \\ 5. & P(2) \rightarrow P(3) & \text{Universal Instantiation (2)} \\ 6. & P(3) & \text{Modus Ponens (4,5)} \\ 7. & P(3) \rightarrow P(4) & \text{Universal Instantiation (2)} \\ 8. & P(4) & \text{Modus Ponens (6,7)} \\ & \vdots & \\ & P(1) \wedge P(2) \wedge \cdots & \text{Conjunction} \\ & \forall n\;P(n) & \text{Definition of } \forall \end{array}

This gives us a proof technique to prove $\forall x\;P(x)$ when the universe of discourse is the natural numbers (starting at either $0$ or $1$). To summarize: $$ \left( P(1) \wedge \left(\forall k\;(P(k) \rightarrow P(k+1))\right) \right) \rightarrow \forall n\;P(n) $$

Why do we need (and like) this?

before, we knew how to prove $\forall x\;(A(x) \rightarrow B(x))$, since we could pick an arbitrary $x$ and attempt a direct proof, but this doesn't always work (easily).
now, we've converted the proof of $\forall n\;P(n)$ into an implication, so we can use a direct proof. By assuming something, we get more leverage.

Proving $P(1)$ is the basis step.

Proving $\forall k\;(P(k) \rightarrow P(k+1))$ is the inductive step.

we will do this for some arbitrary $k$ (as in universal generalization). We do a direct proof, and so we call $P(k)$ the inductive hypothesis and assume that it is true in order to prove $P(k+1)$.
we are not assuming $P(k)$ is true for all positive integers (this is circular reasoning); we are only assuming that $P(k)$ is true for some arbitrary $k$ in the same way we do for a regular direct proof of an implication

Let's show that our guess that the sum of the first $n$ positive odd integers is $n^2$ is correct. Let $P(n)$ denote "the sum of the first $n$ positive itnegers is $n^2$". We want to show $\forall n\;P(n)$ where the universe of discourse is the set of positive integers.

Basis step: We must show $P(1)$. $P(1)$ says that the sum of the first $1$ positive odd integers is $1^2=1$. This is true.
Inductive hypothesis: Assume $P(k)$ is true for an arbitrary $k$. This means that we assume that the sum of the first $k$ positive odd integers is $k^2$: $$ 1+3+5+\cdots+(2k-1)=k^2 $$ \item Inductive step: We must show that $P(k+1)$ is true using the inductive hypothesis. $P(k+1)$ says that the sum of the first $k+1$ positive odd integers is $(k+1)^2$, so let's look at the first $k+1$ positive odd integers: $$ 1+3+5+7+\cdots+(2k-1)+(2k+2) $$ By our inductive hypothesis, $1+3+5+\cdots+(2k-1)=k^2$, so the above expression can be rewritten as $$ k^2 + 2k + 1 $$ Factoring this, we obtain $(k+1)^2$. Therefore, the sum of the first $k+1$ positive odd integers is $(k+1)^2$, and so $P(k+1)$ is true under the assumption that $P(k)$ is true. Therefore, $P(k) \rightarrow P(k+1)$. Since $k$ was arbitrary, $\forall k\;(P(k) \rightarrow P(k+1))$ is true.
By the basis step, we know that $P(1)$ is true. By the inductive step, we know that $\forall k\;(P(k) \rightarrow P(k+1))$ is true. Therefore, $P(1) \wedge \forall k\;(P(k) \rightarrow P(k+1))$ is true, and so by the principle of mathematical induction, $\forall n\;P(n)$ is true, as desired!

A few notes about doing proofs by mathematical induction:

remember the structure: basis step, inductive hypothesis, inductive step
label each part of the proof to help keep things in order
it isn't necessary to define a propositional function, but you can (do not use one unless you state explicitly what it means!)

Induction works with inequalities, too. For example, here is a proof that $n \lt 2^n$ for all positive integers $n$.

Basis step: If $n=1$, then we must show that $1 \lt 2^1 = 2$, which is true.
Inductive hypothesis: Assume that $k \lt 2^k$ for some positive integer $k$.
Inductive step: We must show that $k+1 \lt 2^{k+1}$. We have: $$ k+1 \lt 2^k + 1 \lt 2^k + 2^k \lt 2 \times 2^k = 2^{k+1} $$

Some more notes about doing proofs by mathematical induction:

write out what you must do in the basis and inductive steps
in the inductive step, you must prove $P(k+1)$: thus, you cannot assume it anywhere. Notice that in the last proof, we started with one side of the inequality and derived the other; we did not take $P(k+1)$ and simplify/change it to $P(k)$: that would be the wrong direction!
how do you know when to use mathematical induction?
- look for statements like "for all positive integers" and other signs of universal quantification (where you don't get anywhere by just picking an arbitrary element and attempting universal generalization)

Induction can be used to show things other than equalities/inequalities. For example, here is a proof that $n^3 - n$ is divisble by $3$ for all positive integers $n$:

Basis step: If $n=1$, then we must show that $1^3 - 1 = 1-1 = 0$ is divisible by $3$, which is true.
Inductive hypothesis: Assume that $k^3 - k$ is divisible by $3$ for some positive integer $k$.
Inductive step: We must show that $(k+1)^3 - (k+1)$ is divisible by $3$. We have: \begin{array}{rcl} (k+1)^3 - (k+1) &=& (k^3 + 3k^2 + 3k + 1) - (k+1) \\ &=& (k^3 - k) + (3k^2 +3k + 1 - 1) \\ &=& (k^3 - k) + 3(k^2 + k) \end{array} Notice that the $(k^3 - k)$ is divisible by $3$ by the inductive hypothesis, and $3(k^2+k)$ is divisble by $3$ because there is a factor of $3$. Since the sum of two numbers that are both divisible by $3$ is divisible by $3$, it must be true that $(k+1)^3 - (k+1)$ is divisible by $3$.

There is nothing special about starting at $1$. We can start at any integer $b$ (by using $b$ in our basis step). This will prove the proposition in question true over the universe of discourse $\{b,b+1,b+2,\ldots\}$.

Here is an example with a different basis step. We will prove that $2^0 + 2^1 + 2^2 + 2^3 + \cdots + 2^n = 2^{n+1} - 1$ for all non-negative integers.

Basis step: The smallest non-negative integer is $0$. The left-hand side of the expression is $2^0 = 1$ and the right hand side is $2^1 - 1 = 1-1 = 0$, so the basis step has been proven.
Inductive hypothesis: Assume $2^0 + 2^1 + 2^2 + 2^3 + \cdots + 2^k = 2^{k+1} - 1$ for some non-negative integer $k$.
Inductive step: We must show that $2^0 + 2^1 + 2^2 + 2^3 + \cdots + 2^{k+1} = 2^{k+2} - 1$. We have: \begin{array}{rcl} && 2^0 + 2^1 + 2^2 + 2^3 + \cdots + 2^{k+1} \\ &=& (2^0 + 2^1 + 2^2 + 2^3 + \cdots + 2^k) + 2^{k+1} \\ &=& (2^{k+1} - 1) + 2^{k+1} \\ &=& 2 \times 2^{k+1} - 1 \\ &=& 2^{k+2} - 1 \end{array}

Recall the sum of a geometric sequence $\sum_{j=0}^n ar^j = a + ar + ar^2 + \cdots + ar^n$. We will prove that $\sum_{j=0}^n ar^j = \frac{ar^{n+1} - a}{r-1}$ when $r \neq 1$ and $n \ge 0$.

Basis step: The statement says that $n \ge 0$, so our basis step occurs when $n=0$. The left-hand side is $\sum_{j=0}^0 ar^j = ar^0 = a$, and the right hand side is $$ \frac{ar^1 - a}{r-1} = \frac{ar-a}{r-1} = \frac{a(r-1)}{r-1} = a $$
Inductive hypothesis: Assume that $\sum_{j=0}^k ar^j = \frac{ar^{k+1} - a}{r-1}$ for some non-negative integer $k$.
Inductive step: We must show that $\sum_{j=0}^{k+1} ar^j = \frac{ar^{k+2} - a}{r-1}$. We have: \begin{array}{rcl} \displaystyle \sum_{j=0}^{k+1} ar^j &=& ar^{k+1} + \displaystyle\sum_{j=0}^{k} ar^j \\ &=& ar^{k+1} + \frac{ar^{k+1} - a}{r-1} \\ &=& \frac{(r-1)ar^{k+1}}{r-1} + \frac{ar^{k+1} - a}{r-1}\\ &=& \frac{ar^{k+1} - a + ar^{k+2} - ar^{k+1}}{r-1} \\ &=& \frac{ar^{k+2} - a}{r-1} \\ \end{array}

The $j$-th Harmonic number $H_j$ is defined as $H_j = 1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{j}$ when $j \ge 1$. We will prove that $H_{2^n} \ge 1 + \frac{n}{2}$ for non-negative integers $n$.

Basis step: The statement says that $n \ge 0$, so our basis step occurs when $n=0$. The left-hand side is $H_{2^0} = 1$, and the right hand side is $1 + \frac{0}{2}$, so the statement is true.
Inductive hypothesis: Assume that $H_{2^k} \ge 1 + \frac{k}{2}$ for some non-negative integer $k$.
Inductive step: We must show that $H_{2^{k+1}} \ge 1 + \frac{k+1}{2}$. We have: \begin{array}{rcl} && H_{2^{k+1}} \\ &=& \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{2^k} + \frac{1}{2^k + 1} + \cdots \frac{1}{2^{k+1}} \\ &\ge& \left(1 + \frac{k}{2}\right) + \underbrace{\frac{1}{2^k + 1} + \cdots \frac{1}{2^{k+1}}}_{2^k \text{ terms}} \\ &\ge& \left(1 + \frac{k}{2}\right) + 2^k \times \frac{1}{2^{k+1}} \\ &=& \left(1 + \frac{k}{2}\right) + \frac{1}{2} \\ &=& 1 + \frac{k+1}{2} \\ \end{array}

Recall that the size of the powerset of a set of size $n$ is $2^n$. We will now prove that this is true.

Basis step: If $n=0$, then the set is empty and the only subset is $\emptyset$. Since $2^0 = 1$, the basis step is true.
Inductive hypothesis: Assume that the size of the powerset of a set of size $k$ is $2^k$.
Inductive step: We must show that the size of the powerset of a set of size $k+1$ is $2^{k+1}$.
Let $S$ be a set of $k+1$ elements. Write $S = S' \cup \{ a \}$ where $a \in S$ and $S' = S \setminus \{ a \}$.
- for each subset $X$ of $S'$, there are two subsets of $S$: $X$ and $X \cup \{ a \}$
- since each $X$ is distinct, each $X \cup \{a\}$ is distinct (since $a \notin S'$)
- since $|S| = k+1$, we know that $|S'| = k$. So there are $2^k$ subsets of $S'$ and each produces two subsets of $S$
- therefore, there are $2 \times 2^k = 2^{k+1}$ subsets of $S$

Recall the sum of the first $n$ positive integers: $\sum_{i=1}^n i = \frac{n(n+1)}{2}$. We will now prove that this is true.

Basis step: When $n=1$, we have $\sum_{i=1}^1 i = 1 = \frac{1(2)}{2}$.
Inductive hypothesis: Assume that $\sum_{i=1}^k i = \frac{k(k+1)}{2}$
Inductive step: We must show that $\sum_{i=1}^{k+1} i = \frac{(k+1)(k+2)}{2}$. We have: \begin{array}{rcl} \sum_{i=1}^{k+1} i &=& \left(\sum_{i=1}^k i\right) + (k+1) \\ &=& \frac{k(k+1)}{2} + k + 1 \\ &=& \frac{k(k+1)}{2} + \frac{2(k+1)}{2} \\ &=& \frac{k(k+1) + 2(k+1)}{2} \\ &=& \frac{k^2 + 3k + 2}{2} \\ &=& \frac{(k+1)(k+2)}{2} \end{array}

Here is a proof that $2^n \lt n!$ for all positive integers $n \ge 4$:

Basis step: When $n=4$, we have $2^4 = 16 \lt 24 = 4!$
Inductive hypothesis: Assume that $2^k \lt k!$
Inductive step: We must show that $2^{k+1} \lt (k+1)!$. We have: $$ 2^{k+1} = 2 \times 2^k \lt 2 \times k! \lt (k+1) \times k! = (k+1)! $$

Here is a proof of an extension of De Morgan's Law for sets: $\overline{\bigcap_{j=1}^n A_j} = \bigcup_{j=1}^n \overline{A_j}$, where $A_1,A_2,\ldots,A_n$ are sets and $n \ge 2$:

Basis step: When $n=2$, we have $\overline{A_1 \cap A_2}$ on the left-hand side and $\overline{A_1} \cup \overline{A_2}$ on the right-hand side. This is precisely De Morgan's Law.
Inductive hypothesis: Assume that $\overline{\bigcap_{j=1}^k A_j} = \bigcup_{j=1}^k \overline{A_j}$
Inductive step: We must show that $\overline{\bigcap_{j=1}^{k+1} A_j} = \bigcup_{j=1}^{k+1} \overline{A_j}$. We have: \begin{array}{rcl} \overline{\bigcap_{j=1}^{k+1} A_j} &=& \overline{A_{k+1} \cap \bigcap_{j=1}^{k} A_j} \\ &=& \overline{A_{k+1}} \cup \overline{\bigcap_{j=1}^{k} A_j} \\ &=& \overline{A_{k+1}} \cup \bigcup_{j=1}^{k} \overline{A_j} \\ &=& \bigcup_{j=1}^{k+1} \overline{A_j} \\ \end{array}

Induction can also be used on other types of problems. Let $n$ be a positive integer. We will prove that any $2^n \times 2^n$ chessboard with one square removed can be tiled with L-shaped pieces that cover three squares:

Basis step: When $n=1$, we consider $2 \times 2$ chessboards with one square removed. Here are the four possibilities, along with how they can be covered:
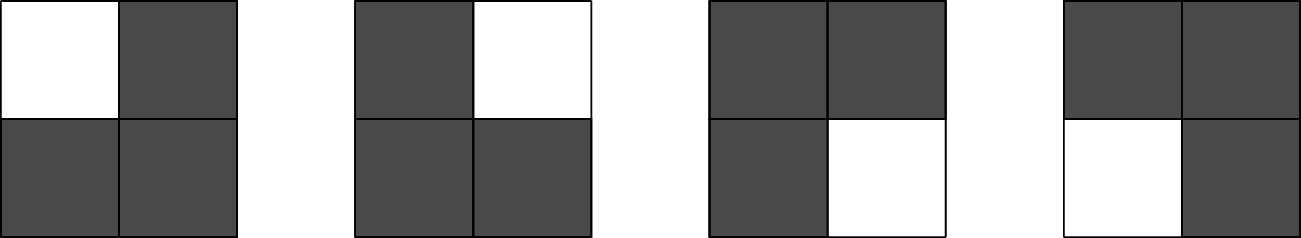
Inductive hypothesis: Assume that any $2^k \times 2^k$ chessboard with one square removed can be tiled with L-shaped pieces.
Inductive step: We must show that any $2^{k+1} \times 2^{k+1}$ chessboard with one square removed can be tiled with L-shaped pieces.
Consider a $2^{k+1} \times 2^{k+1}$ chessboard with one square removed. Divide it in half in both directions to produce four $2^k \times 2^k$ chessboards. The missing square must be in one of these $2^k \times 2^k$ sub-boards. (Let's suppose it is the lower-right, but it does not matter which it is.)

By the inductive hypothesis, the lower-right can be tiled with one square removed. Now, pretend we remove the center squares as illustrated below. The other three sub-boards can be tiled by the inductive hypothesis, and the $2^{k+1} \times 2^{k+1}$ can be tiled by adding in one L-shaped piece in the center.

We will now prove that given $n \ge 2$ lines in the plane (no two of which are parallel), the total number of intersections is at most $\frac{n(n+1)}{2}$. (Recall that non-parallel lines intersect in exactly one point.)

Basis step: If we have $n=2$ non-parallel lines, they intersect in exactly $1 \le \frac{1(2)}{2}$ point.
Inductive hypothesis: Assume that the total number of intersects among $k$ non-parallel lines is at most $\frac{k(k+1)}{2}$.
Inductive step: We must show that the total number of intersects among $k+1$ non-parallel lines is at most $\frac{(k+1)(k+2)}{2}$. Consider any collection of $k+1$ lines. Remove one line. By the inductive hypothesis, there are at most $\frac{k(k+1)}{2}$ intersections. Now add the removed line back. It can intersect each of the $k$ lines at most once, giving at most \begin{array}{rcl} \frac{k(k+1)}{2} + k &=& \frac{k^2 + k}{2} + \frac{2k}{2}\\ &=& \frac{k^2 + 3k}{2}\\ &\le& \frac{k^2 + 3k + 2}{2}\\ &=& \frac{(k+1)(k+2)}{2} \end{array} intersections in total.

Strong Induction

Recall that our argument when doing a proof by induction is the following:

Notice that when we are proving $P(k+1)$, we know more than just $P(k)$; we actually know $P(1) \wedge P(2) \wedge \cdots P(k)$ is true! Therefore, it is valid to use $P(1) \wedge P(2) \wedge \cdots P(k)$ as our inductive hypothesis instead of simply $P(k)$. Using this inductive hypothesis is called strong induction and can (sometimes) make proofs simpler.

We will now look at some examples of proofs that use strong induction.

Consider a game: two players remove any number of matches they want from $1$ of $2$ piles. The player who removes the last match wins the game. The piles initially contain $n \ge 1$ matches each. We will prove that the player who goes second can always win.

Basis step: If $n=1$, then the first player only take one match from one pile, leaving one match in the other. The second player then takes this match and wins.
Inductive hypothesis: If there are $1 \le j \le k$ matches in each pile for some arbitrary $k$, the second player can always win.
Inductive step: Suppose there are $k+1$ matches in each pile. The first player removes $j \ge 1$ matches from one pile, leaving $k+1-j \le k$. The second player then removes the same number of matches from the other pile. At this point, both piles have at most $k$ matches. Thus, by the inductive hypothesis, the second player can win. (Note: it could be that $j=k$, but then the second player can remove all matches in the other pile and win.)

Here is a proof that if $n \gt 1$, then $n$ can be written as a product of prime numbers.

Basis step: If $n=2$, then $n$ is simply the product of itself, which is prime.
Inductive hypothesis: Assume $2 \le j \le k$ can be written as a product of prime numbers for some arbitrary $k$.
Inductive step: We must show that $k+1$ can be written as a product of prime numbers. We consider two cases:
1. If $k+1$ is prime, then it is simply the product of itself, which is prime.
2. If $k+1$ is not prime, then $k+1 = ab$ with $a \le a \le b \lt k+1$. By the inductive hypothesis, $a$ and $b$ are both products of primes, say $a = p_1p_2p_3\cdots$ and $b = q_1q_2q_3\cdots$. We have $$ k+1 = ab = p_1q_1 p_2q_2 p_3q_3 \cdots $$

Notice that in the previous proof, it is not straightforward to apply the original formulation of induction! For some proofs, both techniques apply equally well.

For example, we will prove that every amount of postage greater than or equal to 12¢ can be formed using 4¢ and 5¢ stamps.

Induction:
- Basis step: 12¢ = 3 $\times$ 4¢
- Inductive hypothesis: Assume that a postage of $k$¢ can be formed using 4¢ and 5¢ stamps for some arbitrary $k \ge 12$
- Inductive step: We must show that a postage of $(k+1)$¢ can be formed. Consider postage for $k$¢ from inductive hypothesis. If one 4¢ stamp was used, replace it with a 5¢ stamp to get $(k+1)$¢. Otherwise, the postage for $k$¢ used only 5¢stamps. Since $k \ge 12$, at least 3 $\times$ 5¢ stamps were used. Therefore, if we replace 3 $\times$ 5¢ stamps with 4 $\times$ 4¢ stamps, we get $(k+1)$¢.
Strong Induction
- Basis step: 12¢ = 3 $\times$ 4¢, 13¢ = 2 $\times$ 4¢ $+$ 1 $\times$ 5¢, 14¢ = 1 $\times$ 4¢ $+$ 2 $\times$ 5¢, 15¢ = 3 $\times$ 5¢
- Inductive hypothesis: Assume that a postage of $j$¢ can be formed for $12 \le j \le k$ for some arbitrary $k \ge 15$
- Inductive step: Use stamps for $(k-3)$¢ and add a $4¢$ stamp.

Note that the inductive step in the strong induction proof is only valid because we included the extra cases in the basis step.

Observe that using the usual method of induction resulted in a longer inductive step but shorter basis step, while strong induction resulted in a longer basis step but shorter inductive step.