Discrete Mathematics Study Center

Home Course Notes Exercises Mock Exam About

Relations

Relations between elements of sets are very common. For example:

• sets of people related by the "father" relation
• employees related to companies by the "employed by" relation
• integers related to other integers by the "divisible by" relation
• (...and many other examples)

More formally: let $A$ and $B$ be sets. A binary relation from $A$ to $B$ is a subset of $A \times B$.

Therefore, a binary relation $R$ is just a set of ordered pairs. We write $aRb$ to mean $(a,b) \in R$ and $a \cancel{R} b$ to mean $(a,b) \notin R$. When $(a,b) \in R$, we say that "$a$ is related to $b$ by $R$".

Such relations are binary relations because $A \times B$ consists of pairs. In general, we can have relations that are subsets of $A \times B \times C \times \cdots$ to give us an $n$-ary relation. We concentrate on the binary case.

For example, let $A$ be the set of students at Carleton and $B$ be the set of courses at Carleton. Let $R$ be the "enrolled in" relation, so that $(a,b) \in R$ (that is, $aRb$) if student $a$ is enrolled in course $b$.

Note that you can think of all functions as relations (where the input is related to the output), but not vice versa (since a single element can be related to many others).

Sometimes, relations are between a set $A$ and itself: a subset of $A \times A$. In this case, we say the relation is on the set $A$.

Here are some more examples of relations:

• Let $A = \{1,2,3,4\}$. What ordered pairs are in the relation $R = \{ (a,b) \;|\; a \text{ divides } b \}$? $$ R = \{ (1,1), (1,2), (1,3), (1,4), (2,2), (2,4), (3,3), (3,4) \} $$ This can be represented several ways:

  

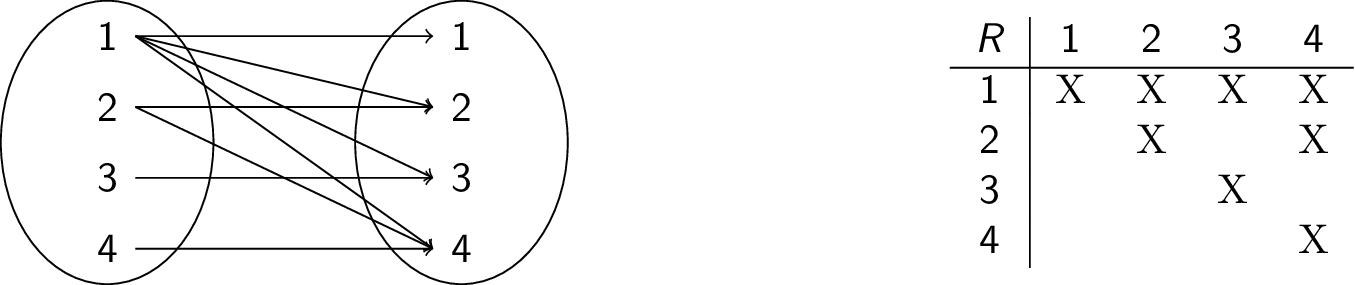
• The following are relations on $\mathbb{Z}$:
  • $R_1 = \{ (a,b) \;|\; a \le b \}$
  • $R_2 = \{ (a,b) \;|\; a \gt b \}$
  • $R_3 = \{ (a,b) \;|\; a = b \text{ or } a = -b \}$
  • $R_4 = \{ (a,b) \;|\; a = b \}$
  • $R_5 = \{ (a,b) \;|\; a = b+1 \}$
  • $R_6 = \{ (a,b) \;|\; a+b \le 3 \}$
  We have:
  • $(1,1) \in R_1,R_3,R_4,R_6$
  • $(1,2) \in R_1,R_6$
  • $(2,1) \in R_2,R_5,R_6$
  • $(1,-1) \in R_2,R_3,R_6$
  • $(2,2) \in R_1,R_3,R_4$

Properties of Relations

Relations can have several properties which help to classify them.

• Reflexivity: a relation $R$ on a set $A$ is reflexive if $(a,a) \in R$ for all $a \in A$.

  For example, if $A = \{1,2,3,4\}$, then:

  • $R_1 = \{ {\bf(1,1)},(1,2),{\bf(2,2)},(2,3),{\bf(3,3)},(3,1),{\bf(4,4)} \}$ is reflexive
  • $R_2 = \{ (1,2),(2,3),(3,4) \}$ is not reflexive since $(1,1) \notin R_2$
  • $R_3 = \{ (1,1),(2,2)(3,3),(1,4) \}$ is not reflexive since $(4,4) \notin R_3$

  As another example, the "divides" relation is reflexive since $a = 1a$ for any integer $a$

• Symmetry: a relation $R$ on a set $A$ is called symmetric if $(a,b) \in R \rightarrow (b,a) \in R$ for all $a,b \in A$
• Antisymmetry: a relation $R$ on a set $A$ is called antisymmetric if $((a,b) \in R \wedge (b,a) \in R) \rightarrow (a=b)$ for all $a,b \in A$.

  Note: symmetry and antisymmetry are not mutually exclusive: a relation can have one, both, or neither. Consider the following relations on $\{1,2,3,4\}$:

  • $R_1 = \{ (1,1),(1,2),(2,1),(2,2),(3,4),(4,1),(4,4) \}$
    • not symmetric: $(3,4) \in R_1$ but $(4,3) \notin R_1$
    • not antisymmetric: $(2,1), (1,2) \in R_1$ but $1 \neq 2$
  • $R_2 = \{ (1,1),(1,2),(1,4),(2,1),(2,2),(3,3),(4,1) \}$
    • symmetric
    • not antisymmetric: $(2,1), (1,2) \in R_2$ but $1 \neq 2
  • $R_3 = \{ (2,1),(3,1),(3,2),(4,1),(4,2),(4,3) \}$
    • not symmetric: $(2,1) \in R_3$ but $(1,2) \notin R_3$
    • antisymmetric
  • $R_4 = \{ (1,1),(2,2) \}$
    • symmetric
    • antisymmetric
• Transitivity: a relation $R$ on a set $A$ is called transitive if, for all $a,b,c \in A$, $$((a,b) \in R \wedge (b,c) \in R) \rightarrow (a,c) \in R$$

  For example, the following relations on $\mathbb{Z}$ are all transitive:

  • $\{ (a,b) \;|\; a \le b \}$
  • $\{ (a,b) \;|\; a \gt b \}$
  • $\{ (a,b) \;|\; a = b \text{ or } a = -b \}$
  • $\{ (a,b) \;|\; a = b \}$

  whereas the following are not:

  • $\{ (a,b) \;|\; a=b+1 \}$
  • $\{ (a,b) \;|\; a+b \le 3 \}$

  The "divides" relation is also transitive. Suppose $a|b$ and $b|c$. Then $b=ka$ and $c=lb$ for integers $k$ and $l$. Therefore, $c = lb = (lk)a$, so $a|c$.

Combining Relations

Relations are sets, so they can be combined the same way sets can be combined.

• Let $A = \{1,2,3\}, B = \{ 1,2,3,4 \}$ and define the relations $R_1 = \{(1,1),(2,2),(3,3)\}$ and $R_2 = \{ (1,1),(1,2),(1,3),(1,4) \}$ from $A$ to $B$ can be combined as follows:
  • $R_1 \cup R_2 = \{ (1,1),(1,2),(1,3),(1,4),(2,2),(2,3)\}$
  • $R_1 \cap R_2 = \{ (1,1) \}$
  • $R_1 \setminus R_2 = \{ (2,2),(3,3) \}$
  • $R_2 \setminus R_1 = \{ (1,2),(1,3),(1,4) \}$
• Let $R_1 = \{ (a,b) \;|\; a \lt b\}$ and $R_2 = \{ (a,b) \;|\; a \gt b \}$ be relations defined on $\mathbb{R}$.
  • $R_1 \cup R_2 = \{(a,b) \;|\; a \lt b \text{ or } a \gt b\} = \{ (a,b) \;|\; a \neq b\}$
  • $R_1 \cap R_2 = \{(a,b) \;|\; a \lt b \text{ and } a \gt b\} = \emptyset$
  • $R_1 \setminus R_2 = R_1$
  • $R_2 \setminus R_1 = R_2$

Remember the relations are like functions, so it makes sense to talk about their composition, too.

Let $R$ be a relation from set $A$ to set $B$. Let $S$ be a relation from set $B$ to set $C$. The composition of $R$ and $S$ is the relation consisting of ordered pairs $(a,c)$ where $a \in A$, $c \in C$ and there exists an element $b \in B$ such that $(a,b) \in R$ and $(b,c) \in S$. We write $S \circ R$ to denote this relation.

For example, if we have a relation $R$ from the set $\{1,2,3\}$ to the set $\{1,2,3,4\}$ and a relation $S$ from the set $\{1,2,3,4\}$ to the set $\{0,1,2\}$ defined as follows:

• $R = \{ (1,1),(1,4),(2,3),(3,1),(3,4) \}$
• $S = \{ (1,0),(2,0),(3,1),(3,2),(4,1) \}$

then $S \circ R = \{ (1,0),(1,1),(2,1),(2,2),(3,0),(3,1) \}$.

One special case of composition occurs when you compose a relation with itself. For example, let $R = \{ (a,b) \;|\; a \text{ is a parent of } b \}$ be defined on the set of all people. Then $R \circ R$ is the set of ordered pairs $(a,c)$ such that there exists a person $b$ so that $a$ is a parent of $b$ and $b$ is a parent of $c$, \ie, $a$ is a grandparent of $c$.

Of course, this produces a new relation which can be composed with $R$ again to produce the "is a great-grandparent of" relation.

As a shortcut, we write $R^2 = R \circ R$, $R^3 = (R \circ R) \circ R)$, and so on.

Let $R = \{ (1,1),(2,1),(3,2),(4,3) \}$. Then:

• $R^1 = R$
• $R^2 = \{ (1,1),(2,1),(3,1),(4,2) \}$
• $R^3 = \{ (1,1),(2,1),(3,1),(4,1) \}$
• $R^4 = R^3$
• $\vdots$
• $R^n = R^3$ for $n \ge 3$

Interestingly, we can understand transitivity in terms of composition: a relation $R$ on a set $A$ is transitive if and only if $R^n \subseteq R$ for $n \ge 1$.

• $(\leftarrow)$: Suppose $R^n \subseteq R$ for $n = 1,2,3,\ldots$. therefore, $R^2 \subseteq R$. Now, if $(a,b) \in R$ and $(b,c) \in R$, then $(a,c) \in R^2$. Since $R^2 \subseteq R$, we must have $(a,c) \in R$. Therefore, $R$ is transitive.
• $(\rightarrow)$: We will use induction to prove this direction.
  • Basis step: ($n=1$) If $R$ is transitive, then $R^1 = R$ is transitive.
  • Inductive hypothesis: Assume $R^k \subseteq R$ for an arbitrary $k$.
  • Inductive step: We want to show that $R^{k+1} \subseteq R$. Suppose that $(a,b) \in R^{k+1}$. Since $R^{k+1} = R^k \circ R$, there must exist an $x \in A$ such that $(a,x) \in R$ and $(x,b) \in R^k$. By the inductive hypothesis, $(x,b) \in R$. Since $R$ is transitive and $(a,x), (x,b) \in R$, we have that $(a,b) \in R$. Since $(a,b)$ was arbitrary, we have that $R^{k+1} \subseteq R$.

Reflexive Closure

Sometimes a relation does not have some property that we would like it to have: for example, reflexivity, symmetry, or transitivity.

How do we add elements to our relation to guarantee the property? Ideally, we'd like to add as few new elements as possible to preserve the "meaning" of the original relation.

We first consider making a relation reflexive. This is called the reflexive closure. Suppose we have a relation $R$ on a set $A$ and want to make it reflexive. We need to ensure that $(a,a)$ is in the relation for all $a \in A$. We also do not wish to add anything extra.

Define $\Delta = \{ (a,a) \;|\; a \in A \}$. The reflexive closure of $R$ is $R \cup \Delta$.

For example, the reflexive closure of $R = \{ (a,b) \;|\; a \lt b \}$ on the set of integers is the relation

$$R \cup \Delta = \{ (a,b) \;|\; a \lt b \} \cup \{ (a,a) \;|\; a \in \mathbb{Z} \} = \{ (a,b) \;|\; a \le b \}$$

Symmetric Closure

For the symmetric closure, we want to ensure that $(b,a)$ is in the closure relation whenever $(a,b)$ is in the original relation.

Define $R^{-1} = \{ (b,a) \;|\; (a,b) \in R \}$. The symmetric closure of $R$ is $R \cup R^{-1}$.

For example, the symmetric closure of $R = \{ (a,b) \;|\; a \lt b \}$ on the set of integers is the relation

$$R \cup R^{-1} = \{ (a,b) \;|\; a \lt b \} \cup \{ (b,a) \;|\; a \gt b \} = \{ (a,b) \;|\; a \neq b \}$$

Transitive Closure

Consider $R = \{ (1,3),(1,4),(2,1),(3,2) \}$ on $A = \{1,2,3,4\}$. This is not a transitive relation: it is missing $\{(1,2),(2,3),(2,4),(3,1) \}$. Let's try adding them and calling the new relation $R'$:

$$R' = \{ (1,3),(1,4),(2,1),(3,2),(1,2),(2,3),(2,4),(3,1) \}$$

Unfortunately, this relation is still not transitive: $(3,1) \in R'$ and $(1,4) \in R'$, but $(3,4) \notin R'$. It seems we will need to do a bit more work.

Recall that if we compose $R$ with itself, then we get the elements $(a,c)$ where $(a,b) \in R$ and $(b,c) \in R$ for some $b$. We need these elements for transitivity, so add them to $R$. As we saw above, this might not be enough, so we repeat this.

How any times do we repeat? This is the same as asking how many intermediate elements we could find. Since there are $|A|$ possible intermediate elements, we might need to do as many as $|A|$ compositions.

Therefore, the transitive closure of $R$ over a set $A$ is

$$R \cup R^2 \cup R^3 \cup \cdots \cup R^{|A|}$$

Here is an example of computing the transitive closure:

• Let $R = \{ (1,1),(1,3),(2,2),(3,1),(3,2) \}$ over the set $A = \{1,2,3\}$. Then:
  • $R^1 = R$
  • $R^2 = \{ (1,1),(1,2),(1,3),(2,2),(3,1),(3,2),(3,3) \}$
  • $R^3 = \{ (1,1),(1,2),(1,3),(2,2),(3,1),(3,2),(3,3) \}$
  The transitive closure of $R$ is $R^1 \cup R^2 \cup R^3$ (since $|A| = 3$): $\{ (1,1),(1,2),(1,3),(2,2),(3,1),(3,2),(3,3) \}$

It turns out we can view this another way if we look at the matrix representation. Given a matrix representations $M_R$ and $M_S$ for the relations $R$ and $S$, the matrix representation of $S \circ R$ is $M_R \odot M_S$, where $\odot$ denotes the join operation. This operation is identical to matrix multiplication, but any non-zero entries are simply written as ones.

The matrix representation of $R$ in the previous example is $$ M_R = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \\ \end{bmatrix} $$

Therefore, we have: $$ M_{R^2} = M_R \odot M_R = \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 0 \\ 1 & 1 & 1 \\ \end{bmatrix} $$ and $$ M_{R^3} = M_{R^2} \odot M_R = \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 0 \\ 1 & 1 & 1 \\ \end{bmatrix} $$

We now take the union of these matrices by taking the logical-or of each entry: $$ \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \\ \end{bmatrix} \vee \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 0 \\ 1 & 1 & 1 \\ \end{bmatrix} \vee \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 0 \\ 1 & 1 & 1 \\ \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 0 \\ 1 & 1 & 1 \\ \end{bmatrix} $$

As we would expect, this is the matrix representation of $\{ (1,1),(1,2),(1,3),(2,2),(3,1),(3,2),(3,3) \}$; the same answer we computed previously.