Sets
A set is an unordered collection of objects.
The objects in a set are called the set's elements or members. They are usually listed inside braces. We write $x \in A$ if $x$ is an element (member) of a set $A$.
$\{1,2,3\}$ is a set with $3$ elements. It is the same as the set $\{1,3,2\}$ (order does not matter) and the set $\{1,1,2,3,3,3,3\}$ (repetition does not matter). Typically, all objects are the same (for example, numbers), but they do not have to be: $\{ 1, 3, \text{red}, \text{blue}, \text{John} \}$ is a set.
Ellipses are used when a pattern is clear: $\{1,2,3,4,\ldots,50\}$ is the set of all integers from $1$ to $50$, inclusive.
Some sets we use a lot:- $\mathbb{R}$ is the set of real numbers
- $\mathbb{N}$ is the set of natural numbers
- $\mathbb{Z}$ is the set of integers
- $\mathbb{Q}$ is the set of rational numbers
It is possible to have a set with no elements: $\{\}$. This is the empty set and is usually denoted $\emptyset$. This is not the same as $\{ \emptyset \}$, which is a set with one element (that happens to be a (empty) set).
The number of distinct elements in a set $S$ is called its cardinality and is denoted $|S|$. If $|S|$ is infinite (for example, $\mathbb{Z}$), we say the set is infinite.
One common way to define a set is set builder notation. Here are two examples:
- $\mathbb{R} = \{ r \;|\; r \text{ is a real number} \}$
- $O = \{ x \;|\; x \text{ is an odd integer} \}$
Set Operations
Several operations can be performed on sets.-
Union: Given two sets $A$ and $B$, the union $A \cup B$ is the set of all elements that are in either $A$ or $B$. For example, if $A = \{ 1,3,5 \}$ and $B = \{ 2,3,6 \}$, then $A \cup B = \{ 1,2,3,4,5,6 \}$. Note that $A \cup B = \{ x \;|\; (x \in A) \lor (x \in B) \}$.
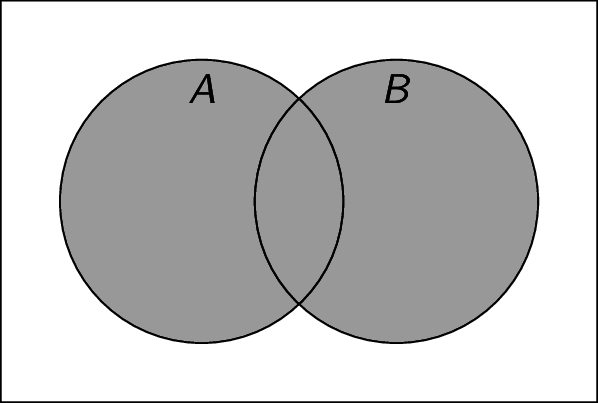
-
Intersection: Given two sets $A$ and $B$, the intersection $A \cap B$ is the set of all elements that are in both $A$ and $B$. For example, if $A = \{ 1,2,3,4 \}$ and $B = \{ 3,4,5,6 \}$, then $A \cap B = \{ 3,4 \}$. Note that $A \cap B = \{ x \;|\; (x \in A) \land (x \in B) \}$. We say that $A$ and $B$ are disjoint if $A \cap B = \emptyset$.

-
Difference: Given two sets $A$ and $B$, the difference $A \setminus B$ is the set of all elements that are in $A$ but not in $B$. For example, if $A = \{ 1,2,3,4 \}$ and $B = \{ 3,4 \}$, then $A \setminus B = \{ 1,2 \}$. Note that $A \setminus B = \{ x \;|\; (x \in A) \land (x \notin B) \}$. $A \setminus B$ is also denoted $A - B$.
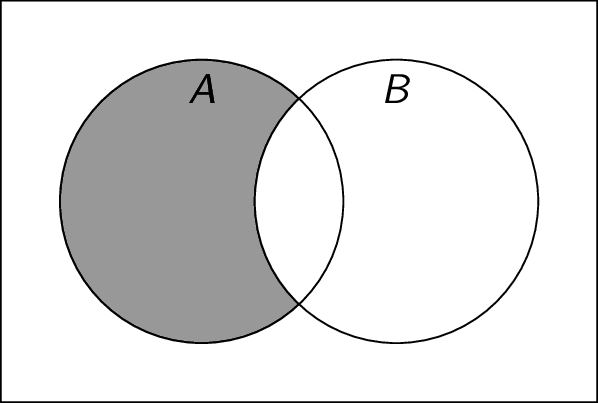
-
Complement: Given a set $A$, the complement $\overline{A}$ is the set of all elements that are not in $A$. To define this, we need some definition of the universe of all possible elements $U$. We can therefore view the complement as a special case of set difference, where $\overline{A} = U \setminus A$. For example, if $U = \mathbb{Z}$ and $A = \{ x \;|\; x \text{ is an odd integer} \}$, then $\overline{A} = \{ x \;|\; x \text{ is an even number} \}$. Note that $\overline{A} = \{ x \;|\; x \notin A \}$.
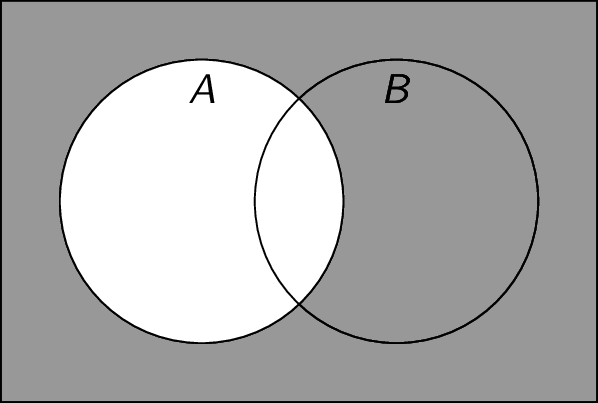
- Cartesian Product: Given two sets $A$ and $B$, the cartesian product $A \times B$ is the set of ordered pairs where the first element is in $A$ and the second element is in $B$. We have $A \times B = \{ (a,b) \;|\; a \in A \land b \in B \}$. For example, if $A = \{ 1,2,3 \}$ and $B = \{ a,b \}$, then $A \times B = \{ (1,a),(1,b),(2,a),(2,b),(3,a),(3,b) \}$.
Subsets
A set $A$ is a subset of a set $B$ if every element of $A$ is an element of $B$. We write $A \subseteq B$. Another way of saying this is that $A \subseteq B$ if and only if $\forall x\;(x \in A \rightarrow x \in B)$.
For any set S, we have:
-
$\emptyset \subseteq S$
Proof: Must show that $\forall x\;{(x \in \emptyset \rightarrow x \in S)}$. Since $x \in \emptyset$ is always false, the implication is always true. This is an example of a trivial or vacuous proof.
-
$S \subseteq S$
Proof: Must show that $\forall x\;{(x \in S \rightarrow x \in S)}$. Fix an element $x$. We must show that $x \in S \rightarrow x \in S$. This implication is equivalent to $x \in S \lor x \notin S$, which is a tautology. Therefore, by Universal Generalization, $S \subseteq S$.
Power Sets
The power set of a set $A$ is the set of all subsets of $A$, denoted $\mathcal{P}(A)$. For example, if $A = \{1,2,3\}$, then $\mathcal{P}(A) = \{ \emptyset, \{1\},\{2\},\{3\}, \{1,2\},\{2,3\},\{1,3\}, \{1,2,3\} \}$
Notice that $|\mathcal{P}(A)| = 2^{|A|}$.
Set Equality
Two sets are equal if they contain the same elements. One way to show that two sets $A$ and $B$ are equal is to show that $A \subseteq B$ and $B \subseteq A$:
\begin{array}{lll} A \subseteq B \land B \subseteq A & \equiv & \forall x\;{((x \in A \rightarrow x \in B) \land (x \in B \rightarrow x \in A))} \\ &\equiv & \forall x\;{(x \in A \leftrightarrow x \in B)} \\ &\equiv & A = B \\ \end{array}Note: it is not enough to simply check if the sets have the same size! They must have exactly the same elements. Remember, though, that order and repetition do not matter.