Discrete Mathematics Study Center

Home Course Notes Exercises Mock Exam About

Mock Exam

Please select one answer for each of the following questions. At the bottom of the page, you will be able to grade your answers, as well as see the correct response to each question. This mock exam is based on a previous exam that students were given three hours to complete.

1. Which of the following sentences is a proposition?
   1. "Are you ready for this exam?"
   2. "This exam has 41 questions."
   3. "Good luck!"
   4. "$a+b = 5$"
2. What is the negation of the proposition "The summer in Ottawa is sunny and warm."?
   1. "The summer in Ottawa is not sunny and not warm."
   2. "The summer in Ottawa is either sunny or warm."
   3. "The summer in Ottawa is either not sunny or not warm."
   4. "The winter in Ottawa is sunny and warm."
3. What is the negation of the proposition "If the exam is easy, then I am happy."?
   1. "The exam is easy but I am not happy."
   2. "If I am happy, then the exam is easy."
   3. "If the exam is not easy, then I am not happy."
   4. "If I am not happy, then the exam is not easy."
4. What is the contrapositive of the implication "If the exam is easy, then I am relaxed and happy."?
   1. "If the exam is not easy, then I am not relaxed or I am not happy."
   2. "If the exam is not easy, then I am not relaxed and I am not happy."
   3. "If I am not relaxed and I am not happy, then the exam is not easy."
   4. "If I am not relaxed or I am not happy, then the exam is not easy."
5. Consider the proposition $((p \rightarrow q) \wedge (\neg r \rightarrow \neg q)) \rightarrow (\neg p \vee r)$. This proposition is a:
   1. tautology
   2. contradiction
   3. contingency
   4. none of the above
6. Consider the proposition $\neg((a \rightarrow \neg b) \rightarrow (b \rightarrow \neg a))$. This proposition is a:
   1. tautology
   2. contradiction
   3. contingency
   4. none of the above
7. Which of the following pairs of propositions are logically equivalent?
   1. $(p \rightarrow q) \rightarrow r$ and $p \rightarrow (q \rightarrow r)$
   2. $(p \wedge q) \rightarrow r$ and $(p \rightarrow r) \wedge (q \rightarrow r)$
   3. $\neg p \rightarrow (q \rightarrow r)$ and $q \rightarrow (p \vee r)$
   4. $(p \rightarrow q) \rightarrow (q \rightarrow r)$ and $(p \rightarrow r) \rightarrow (q \rightarrow r)$
8. Which of the following pairs of propositions are logically equivalent?
   1. $(p \rightarrow q) \vee (p \rightarrow r)$ and $p \rightarrow (q \wedge r)$
   2. $(p \rightarrow q) \vee (p \rightarrow r)$ and $p \rightarrow (q \vee r)$
   3. $(p \rightarrow q) \vee (p \rightarrow r)$ and $p \rightarrow (q \wedge \neg r)$
   4. $(p \rightarrow q) \vee (p \rightarrow r)$ and $p \rightarrow (\neg q \wedge r)$
9. Let $C(x,y)$ be a propositional function that depends on $x$ and $y$. What is the negation of $\forall x \exists y\;C(x,y)$?
   1. $\exists x \forall y\; \neg C(x,y)$
   2. $\forall x \exists y\; \neg C(x,y)$
   3. $\exists x \exists y\; \neg C(x,y)$
   4. $\forall x \forall y\; \neg C(x,y)$
10. Suppose the universe of discourse is the set of positive integers. Let $C(x,y)$ denote "$x \le y$". What is the negation of the proposition "There exists a number that is less than or equal to all numbers."?
    1. $\exists x \forall y\; \neg C(x,y)$
    2. $\neg(\exists x \forall y\; C(x,y))$
    3. $\neg(\forall x \exists y\; C(x,y))$
    4. $\forall x \forall y\; \neg C(x,y)$
11. Consider the following premises: If you do not buy food, then you do not eat. If you buy food, then you have money. If you have money, then you have a job. You do not have a job. What is a valid conclusion to infer from these premises?
    1. You eat.
    2. You buy food.
    3. You do not eat.
    4. You have money.
12. Consider the following premises, where the universe of discourse is the set of all people: Everyone who enjoys french fries also enjoys burgers. Everyone who enjoys burgers is not a vegetarian. At least one student in this class enjoys french fries. What is a valid conclusion to infer from these premises?
    1. Every student in this class is a vegetarian.
    2. Every student in this class is not a vegetarian.
    3. At least one student in this class is a vegetarian.
    4. At least one student in this class is not a vegetarian.
13. Consider the following argument with premise $\forall x \; (P(x) \vee Q(x))$ and conclusion $(\forall x \; P(x)) \wedge (\forall x \; Q(x))$. \begin{array}{lll} 1. & \forall x \; (P(x) \vee Q(x)) & \therefore (\forall x \; P(x)) \wedge (\forall x \; Q(x)) \\\hline 2. & P(c) \vee Q(c) & \text{Universal Instantiation of 1} \\ 3. & P(c) & \text{Simplification of 2} \\ 4. & \forall x \; P(x) & \text{Universal Generalization of 3} \\ 5. & Q(c) & \text{Simplification of 2} \\ 6. & \forall x \; Q(x) & \text{Universal Generalization of 5} \\ 7. & (\forall x \; P(x)) \wedge (\forall x \; Q(x)) & \text{Conjunction of 4 and 6} \\ \end{array}
    1. This is a valid argument.
    2. Steps 3 and 5 are not correct inferences.
    3. Steps 4 and 6 are not correct inferences.
    4. Step 7 is not a correct inference.
14. Let $A = \{a, c, 4, \{4,5\}, \{1, 4, 3, 3,2\}, d,e, \{3\}, \{4\}\}$. Which of the following statements is true?
    1. $\{a, c, 4\} \subseteq A$ and $\{4,5\} \in A$.
    2. $\{a, c, 4\} \subseteq A$ and $\{4,5\} \subseteq A$.
    3. $\{a, c, 4\} \in A$ and $\{4,5\} \in A$.
    4. $\{a, c, 4\} \in A$ and $\{4,5\} \subseteq A$.
15. Let $A = \{a, c, 4, \{4,5\}, \{1, 4, 3, 3,2\}, d,e, \{3\}, \{4\}\}$. Which of the following statements is true?
    1. $\{1, 4, 3, 2\} \subseteq A$ and $\{4,\{4\}\} \subseteq A$.
    2. $\{1, 4, 3, 2\} \in A$ and $\{4,\{4\}\} \in A$.
    3. $\{1, 4, 3, 2\} \subseteq A$ and $\{4,\{4\}\} \in A$.
    4. $\{1, 4, 3, 2\} \in A$ and $\{4,\{4\}\} \subseteq A$.
16. Let $A = \{x, y, 7, \{7,5\}, \{6, 7, 3, 3,2\}, u,v, \{3\}, \{7\}\}$. What is $|A|$ (i.e., the cardinality of $A$)?
    1. $9$
    2. $11$
    3. $13$
    4. $14$
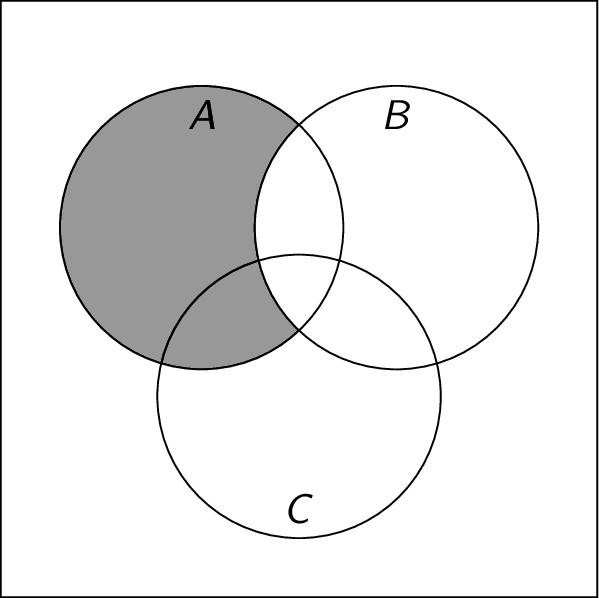
17. Which set does the following Venn diagram represent?

    

    1. $\overline{(C\cap\overline{B})}\cup(C\cap\overline{A})$
    2. ${(C\cap\overline{A})}\cap\overline{(B\cap\overline{A})}$
    3. $(A\cap\overline{B})\cap {(C\cup A)}$
    4. $\overline{(A\cap\overline{B})}\cup(C\cap\overline{A})$
18. Let $f$ be a function from the set of real numbers to the set of real numbers defined by $f(x) = -3x^2$.
    1. $f$ is injective but not surjective.
    2. $f$ is surjective but not injective.
    3. $f$ is neither surjective nor injective.
    4. $f$ is both injective and surjective.
19. Let $f$ be a function from the set of real numbers to the set of real numbers defined by $f(x) = -5x^3$.
    1. $f$ is injective but not surjective.
    2. $f$ is surjective but not injective.
    3. $f$ is neither surjective nor injective.
    4. $f$ is both injective and surjective.
20. Let $f$ be a function whose domain and codomain are the set $\{a,b,c,d,e,f,g\}$. Assume that $f(a)=g$, $f(b)=b$, $f(c)=a$, $f(d)=g$, $f(e)=f$, $f(f)=c$, and $f(g)=d$.
    1. $f$ is injective but not surjective.
    2. $f$ is surjective but not injective.
    3. $f$ is neither surjective nor injective.
    4. $f$ is a bijection.
21. Which of the following sets is uncountable?
    1. The set $(A \times A) \times A$, where $A$ is a countable set.
    2. The set of negative integers.
    3. The set of real numbers between $0$ and $\frac{1}{1000000}$.
    4. The set of integers that are multiples of $7$.
22. Evaluate the sum $\sum_{i=1}^{n}(i^2-\frac{1}{3}i+3)$.
    1. $\frac{n^3+n^2+9n}{3}$
    2. $\frac{n^2+6n+1}{6}$
    3. $\frac{n^3+n^2+3n+1}{6}$
    4. $\frac{n^3+n^2+3n}{2}$
23. Let $f(n) = 34n^4 - 71n^3 + 18n + 200$ and $g(n) = 18n^7 + 17n^5 - 879$. Which of the following is true?
    1. $f(n)$ is $O(n^4)$ and $g(n)$ is $\Theta(n^7)$.
    2. $f(n)$ is $O(n^3)$ and $g(n)$ is $O(n^7)$.
    3. $f(n)$ is $\Theta(n^5)$ and $g(n)$ is $\Theta(n^7)$.
    4. $f(n)$ is $O(n^5)$ and $g(n)$ is $\Omega(n^8)$.
24. Let $f(n) = 3n^2 - 5n + 1$. Which of the following values of $c$ and $k$ show that $f(n)$ is $\Omega(n^2)$?
    1. $c=2$ and $k=5$
    2. $c=2$ and $k=4$
    3. $c=3$ and $k=5$
    4. $c=3$ and $k=4$
25. Suppose you are trying to prove the statement $P(n)$ is true for every integer $n \ge 1$. You already know that $P(1)$ is true. How do you complete the proof?
    1. Assume that $P(k)$ is true for every $k \ge 1$ and show that $P(k+1)$ is true.
    2. Assume that $P(k)$ is true for some $k \ge 1$ and show that $P(k+1)$ is true for every $k \ge 1$.
    3. Assume that $P(k)$ is true for some $k \ge 1$ and show that $P(k+1)$ is true.
    4. None of the above techniques will work.
26. Suppose you are trying to prove the statement "$n^3 + 2n$ is divisible by $3$ for every positive integer $n$" by induction. What value of $n$ should be used for the basis step?
    1. $n=0$
    2. $n=1$
    3. $n=2$
    4. $n=3$
27. Consider the following inductive step of a proof by induction of the statement "$n^3 + 2n$ is divisible by $3$ for every positive integer $n$" by induction.

    Assume that $k^3 + 2k$ is divisible by $3$ for some $k \ge 1$. We want to show that $(k+1)^3 + 2(k+1)$ is divisible by $3$. We have that: \begin{array}{rcl} (k+1)^3 + 2(k+1) &=& k^3 + 3k^2 + 3k + 1 + 2k + 2\\ &=& (k^3 + 2k) + (3k^2 + 3k + 3) \end{array} $(k^3 + 2k)$ is divisible by $3$ because $\underline{\hspace{0.5in}(1)\hspace{0.5in}}$. $(3k^2 + 3k + 3)$ is divisible by $3$ because $\underline{\hspace{0.5in}(2)\hspace{0.5in}}$. Therefore, $(k+1)^3 + 2(k+1)$ is divisible by $3$.

    1. Statement (1) could be "of the inductive hypothesis", Statement (2) could be "all terms have common factor $3$"
    2. Statement (1) could be "all terms have common factor $3$", Statement (2) could be "of the inductive hypothesis"
    3. Statement (1) could be "of the inductive hypothesis", Statement (2) could be "of the inductive hypothesis"
    4. Statement (1) could be "all terms have common factor $3$", Statement (2) could be "all terms have common factor $3$"
28. Recall that $H_n$ is the $n$-th harmonic number: $H_n = 1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n}$. Suppose we are trying to prove that $H_{2^n} \le 1 + n$ for all non-negative integers $n$ by induction. In the inductive step, we must show that $H_{2^{k+1}} \le 1 + (k+1)$. Which of the following is a reasonable first step in this part of the proof?
    1. $H_{2^{k+1}} = H_{2^k} + H_{2^k + 1}$
    2. $H_{2^{k+1}} = H_{2^k} + H_{2^{k+1}}$
    3. $H_{2^{k+1}} = H_{2^k} + \frac{1}{2^k + 1} + \frac{1}{2^k + 2} + \cdots + \frac{1}{2^k+2^k}$
    4. $H_{2^{k+1}} = H_{2^k} + \frac{1}{2^{k+1}} + \frac{1}{2^{k+2}} + \cdots + \frac{1}{2^{k+k}}$
29. Let $A=\{a,b,c,d,e,f,g,h\}$ and $R = \{(a,a), (b,b), (c,d), (c,g), (d,g), (e,h), (f,f), (g,g) \}$ be a relation on $A$. Then $R$ is:
    1. reflexive and symmetric
    2. antisymmetric and not reflexive
    3. reflexive and antisymmetric
    4. symmetric and not reflexive
30. The matrix below defines an equivalence relation on the set $\{ a,b,c,d,1,2,3,4,x,y,z \}$. Each "$1$" indicates an element of the relation; for example, $(3,d)$ is in the relation, because the entry in row $3$ and column $d$ has a "$1$". Each "$0$" indicates an element that is not in the relation; for example, $(d,4)$ is not in the relation, because the entry in row $d$ and column $4$ has a "$0$". \begin{array}{c|ccccccccccc} & a & b & c & d & 1 & 2 & 3 & 4 & x & y & z \\ \hline a & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ b & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ c & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ d & 0 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 3 & 0 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 4 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ x & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ y & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ z & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ \end{array} Which of the following sets is an equivalence class of this relation?
    1. $\{a,b,c,d\}$
    2. $\{1,2,3\}$
    3. $\{x,y,z\}$
    4. $\{a,b,c,d,1,2,3,4,x,y,z\}$

31. 

    In the above Hasse diagram, which of the following statements is true?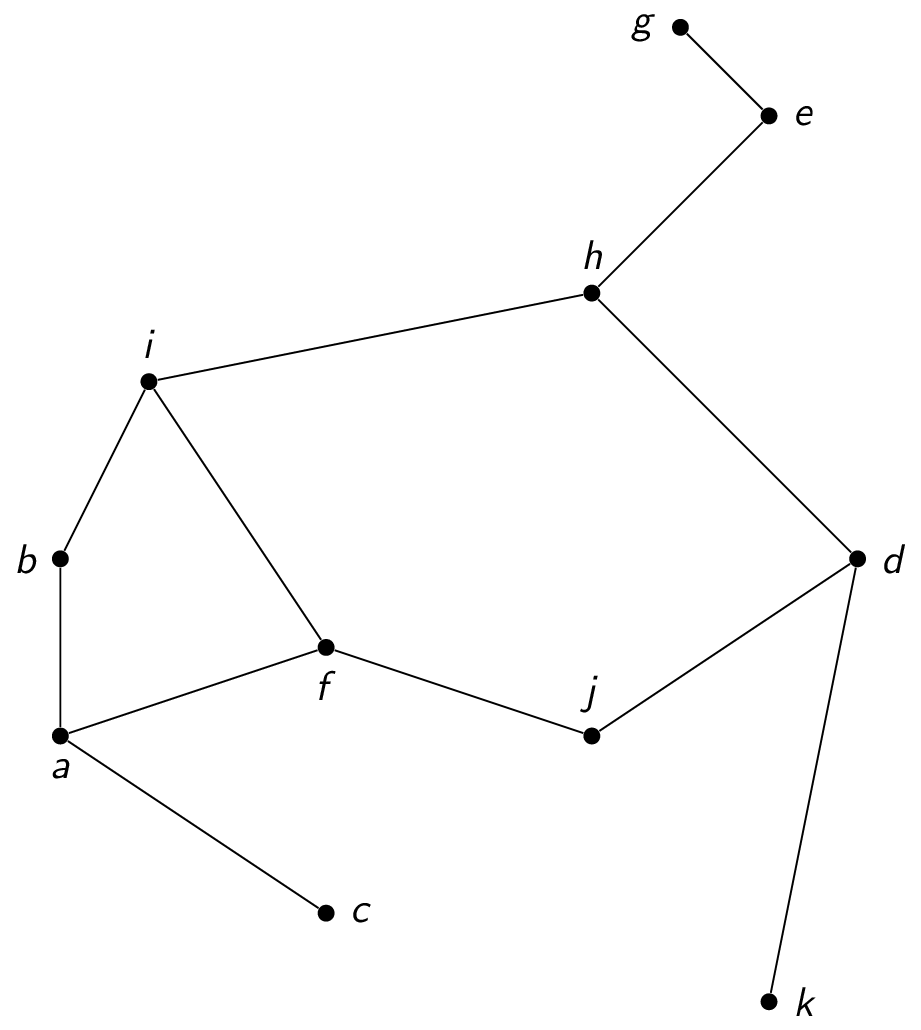
    1. $k$ is a minimal element and $c$ is a maximal element
    2. $g$ is a minimal element and $k$ is a maximal element
    3. $j$ is a minimal element and $g$ is a maximal element
    4. $c$ is a minimal element and $e$ is a maximal element
32. In the above Hasse diagram, which of the following is the least element?
    1. $c$
    2. $k$
    3. $j$
    4. there is no least element
33. In the above Hasse diagram, which of the following is the greatest element?
    1. $g$
    2. $e$
    3. $h$
    4. there is no greatest element
34. In the above Hasse diagram, what are the upper bounds of $\{f,b\}$?
    1. $\{i,h,e,g\}$
    2. $\{a,c\}$
    3. $\{c,j,k\}$
    4. $\{g\}$
35. Which of the following total orders is compatible with the partial order represented by the above Hasse diagram?
    1. $a,b,c,d,e,f,g,h,i,j,k$
    2. $c,a,b,i,e,d,k,j,f,h,g$
    3. $g,a,b,k,d,j,f,i,h,e,c$
    4. $k,j,d,c,a,f,b,i,h,e,g$

36. 

    How could the above graph be classified?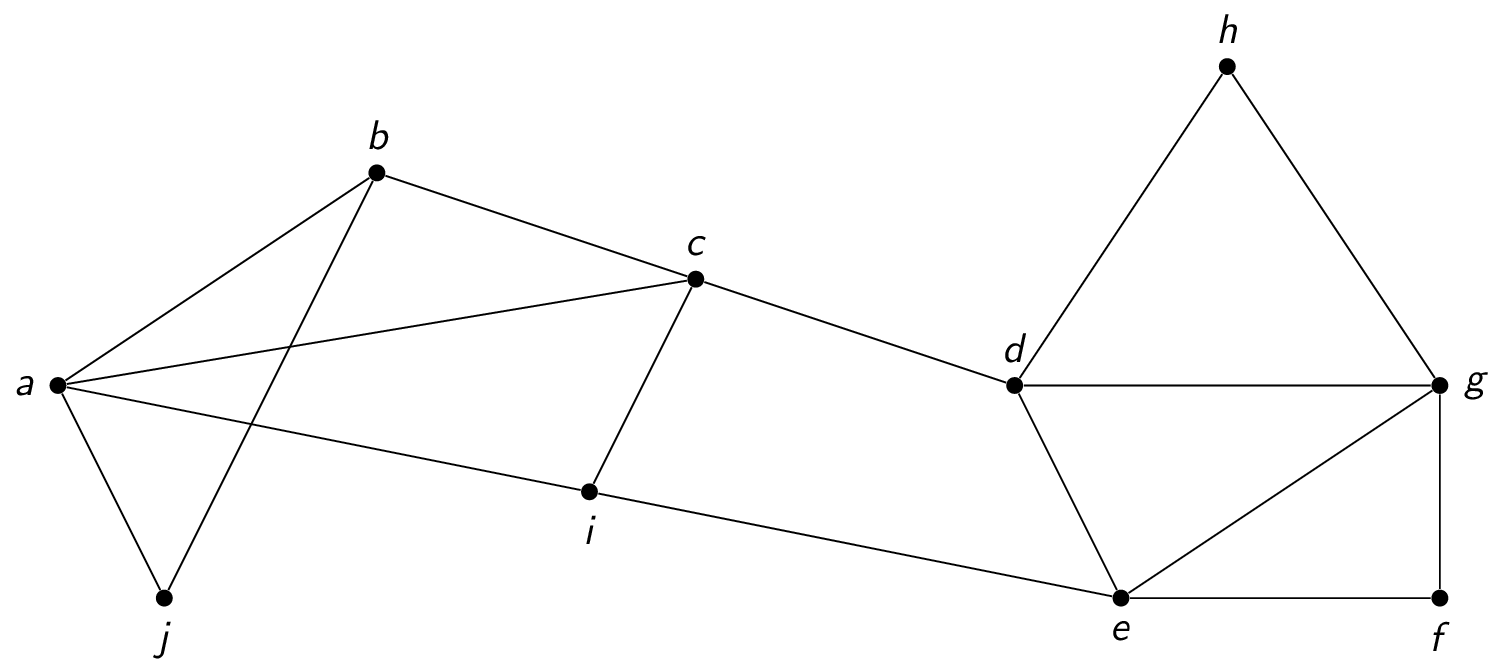
    1. as an undirected simple graph
    2. as a directed simple graph
    3. as a multigraph that is not simple
    4. as a pseudograph that is not simple
37. In the above graph, which of these vertices has degree $3$?
    1. $c$
    2. $b$
    3. $f$
    4. $d$
38. Suppose a depth-first search (DFS) is performed on the above graph starting at vertex $i$. Suppose further that first vertex reached after $i$ is $c$. How many tree edges will be incident to vertex $c$ once the algorithm has finished?
    1. $1$
    2. $2$
    3. $3$
    4. $4$
39. Suppose a breadth-first search (BFS) is performed on the above graph starting at vertex $f$. What is the depth (distance) of vertex $c$ with respect to the starting vertex $f$?
    1. $1$
    2. $2$
    3. $3$
    4. $4$
40. The above graph is planar.
    1. True
    2. False

When you are satisified with your answers, please click the "Compute Grade" to determine your grade on the mock exam. You can show or hide the correct answers with the "Show Answers" and "Hide Answers" buttons.