Discrete Mathematics Study Center

Home Course Notes Exercises Mock Exam About

Equivalence Relations

We intuitively know what it means to be "equivalent", and some relations satisfy these intuitions, while others do not.

Consider the usual "$=$" relation. This is a perfectly good relation: we usually write $1=1$, for example, but can define $R = \{ (a,b) \;|\; a=b \}$ on $\mathbb{Z}$, and write $(1,1) \in R$ or $1R1$.

Why do we say the "$=$" relation expresses equivalence?

• anything is equivalent to itself (reflexive)
• if $a=b$ then $b=a$ (symmetric)
• if $a=b$ and $b=c$, then $a=c$ (transitive)

Other examples include logical equivalence, set equivalence, and many others.

A relation is an equivalence relation if it is reflexive, symmetric and transitive.

To show something is an equivalence relation, just show that it has all of these properties. To show a relation is not an equivalence relation, show it does not satisfy at least one of these properties.

Here are some examples of determining if relations are equivalence relations:

• $R = \{ (a,b) \;|\; a=b \text{ or } a = -b \}$ over $\mathbb{Z}$
  • reflexive: $a = a$, so $(a,a) \in R$
  • symmetric: assume $(a,b) \in R$. Then $a=b$ or $a=-b$. If $a=b$, then $b=a$ so $(b,a) \in R$. If $a = -b$, then $b = -a$, so $(b,a) \in R$.
  • transitive: assume $(a,b) \in R$ and $(b,c) \in R$. Then $a=b$ or $a=-b$ and $b=c$ or $b=-c$.
    • if $a=b$ and $b=c$, then $a=c$ so $(a,c) \in R$
    • if $a=b$ and $b=-c$, then $a=-c$ so $(a,c) \in R$
    • if $a=-b$ and $b=c$ then $-b=-c$, so $a=-b=-c$, so $(a,c) \in R$
    • if $a=-b$ and $b=-c$ then $-b=c$, so $a=-b=c$, so $(a,c) \in R$
• $R = \{ (a,b) \;|\; m \text{ divides } a-b \}$ (for some $m \in \mathbb{Z}^+$) over $\mathbb{Z}$
  • reflexive: $m$ divides $a-a=0$ since $0 = 0 \times m$
  • symmetric: assume $(a,b) \in R$. Then $m$ divides $a-b$. So $a-b = km$ for some integer $k$. Therefore, $-(a-b) = -km$, so $b-a = (-k)m$ and $m$ divides $b-a$, so $(b,a) \in R$.
  • transitive: assume $(a,b) \in R$ and $(b,c) \in R$. Then $a-b = k_1m$ and $b-c = k_2m$. Adding these two equations together gives $(a-b)+(b-c) = k_1m + k_2m$, or $a-c = (k_1+k_2)m$, so $m$ divides $a-c$ and $(a,c) \in R$
• $R$ is a relation on sets of strings of English letters such that $(a,b) \in R$ iff $a$ and $b$ have the same length
  • reflexive: any string has the same length as itself
  • symmetric: if $(a,b) \in R$ then the length of $a$ is the same as the length of $b$, $(b,a) \in R$ as well
  • transitive: assume $(a,b) \in R$ and $(b,c) \in R$. Then the lengths of $a$, $b$, and $c$ are all the same. In particular, the lengths of $a$ and $c$ are the same, so $(a,c) \in R$
• Is the divides relation on the integers an equivalence relation?
  • reflexive: $a|a$ since $a = 1 \times a$
  • transitive: if $a|b$ and $b|c$, we know that $b=k_1a$ and $c=k_2b$, so $c = k_1b = k1(k_2)a = (k_1k_2)a$, so $a|c$
  • symmetric: the relation is not symmetric since $2|4$ but $4$ does not divide $2$
  Since the divides relation is not symmetric, it is not an equivalence relation!
• $R = \{ (a,b) \;|\; |a-b| \lt 1 \}$ over $\mathbb{R}$
  • reflexive: $a-a = 0 \lt 1$
  • symmetric: if $(a,b) \in R$ then $|a-b| \lt 1$. Since $|a-b| = |b-a|$, we have that $|b-a| \lt 1$
  • transitive: if $x = 2.8$, $y=1.9$, $z=1.1$, then
    • $|x-y| = |2.8-1.9| = 0.9 \lt 1$, so $(x,y) \in R$
    • $|y-z| = |1.9-1.1| = 0.8 \lt 1$, so $(y,z) \in R$
    • $|x-z| = |2.8-1.1| = 1.7 \ge 1$, so $(x,z) \notin R$
  Therefore, the relation is not transitive and thus it is not an equivalence relation.

Equivalence Classes

Equivalence relations naturally partition the elements of the set they are defined on into several classes.

For example, let $R = \{ (a,b) \;|\; a \text{ got the same grade as } b \text{ in this course} \}$ over the set of students in this course. It is clear that $R$ is an equivalence relation. Observe that it also partitions the students in this course into classes: A+, A, A-, B+, and so on.

Let $R$ be an equivalence relation on a set $A$. The set of all elements related by $R$ to $a$ is called the equivalence class of $a$ and is denoted $[a]_R$ (or $[a]$ when $R$ is clear from context): $$[a]_R = \{ b \;|\; (a,b) \in R \}$$

If $b \in [a]_R$, then $b$ is called a representative of the equivalence class. Any member of the class can be chosen to be a representative.

Here are some examples of working with equivalence classes:

• Recall $R = \{ (a,b) \;|\; a=b \text{ or } a=-b \}$ is an equivalence relation over $\mathbb{Z}$. An integer is equivalent to itself and its negative, so we have $[a] = \{a,-a\}$. In particular, $[1] = \{1,-1\}, [2] = \{2,-2\}$, and so on. Note that $[0] = \{0\}$
• Let $R = \{ (a,b) \;|\; a \text{ and } b \text{ have the same first letter} \}$ over the set of English words. This is an equivalence relation, and they equivalene classes are all words starting with "a", all words starting with the letter "b", and so on.

In the grades example we saw before, the equivalence classes were the students who achieved the same grade. Notice that this is a partition: two equivalence classes are either equal or disjoint, and the union of all equivalence classes is the set over which the relation is defined.

This works the other way, too: given a partition of a set $A$, we can always construct an equivalence relation $R$ on $A$ with those equivalence classes.

• Suppose we partition $A = \{1,2,3,4,5,6\}$ into $A_1 = \{1\}, A_2 = \{2,3\}, A_3 = \{4,5,6\}$. Define an equivalence relation on $A$ with equivalence classes $A_1,A_2,A_3$.

  To do this, we simply define the relation to ensure that each element in subset is related to every other element in the subset:

  • $R_1 = \{ (a,b) \;|\; a,b \in A_1 \} = \{ (1,1) \}$
  • $R_2 = \{ (a,b) \;|\; a,b \in A_2 \} = \{ (2,2),(2,3),(3,2),(3,3) \}$
  • $R_3 = \{ (a,b) \;|\; a,b \in A_3 \} = \{ (4,4), (4,5), (4,6), (5,4), (5,5), (5,6),(6,4), (6,5), (6,6) \}$

  Taking the union $R_1 \cup R_2 \cup R_3$ gives the desired relation $R$.

Partial Orders

A relation $R$ on a set $A$ is called a partial ordering or partial order if it is reflexive, antisymmetric, and transitive. A set $A$ together with a partial order $R$ on that set is called a partially ordered set or poset and is denoted $(A,R)$. Members of $A$ are called elements of the poset.

Here are some examples:

• The $\ge$ relation on $\mathbb{Z}$ is a partial order:
  • reflexive: $a \ge a$ for all $a \in \mathbb{Z}$
  • antisymmetric: if $a \ge b$ and $b \ge a$, then $a=b$
  • transitive: if $a \ge b$ and $b \ge c$, then $a \ge c$
  Therefore, $\ge$ is a partial order. Notice that $>$ would not be a partial order because it is not reflexive.
• We saw in the last section that the "divides" relation on $\mathbb{Z}^+$ is reflexive and transitive. Is it antisymmetric?

  Yes. If $a|b$ and $b|a$, then $b = ak_1$ and $a = bk_2$, so $b = bk_1k_2$, so $k_1k_2 = 1$. Since $k_1, k_2 \in \integers^+$, $k_1 = k_2 = 1$, and so $b=ak_1=a$.

In a partial order, we cannot always compare two elements. The elements $a,b$ of a poset $(S,\preceq)$ are comparable if either $a \preceq b$ or $b \preceq a$. When neither is true, they are incomparable.

• In the "divides" relation, $5$ does not divide $7$ and $7$ does not divide $5$, so they are incomparable. However, $2$ divides $4$ so $2$ and $4$ are comparable.
• In the $\le$ relation, we always have $a \le b$ or $b \le a$, so every pair of elements is comparable.

The fact that we can have incomparable elements is why the relations are called partial orderings.

If $(S,\preceq)$ is a poset and every two elements of $S$ are comparable, $S$ is called a totally ordered set or a linearly ordered set and $\preceq$ is called a total order or linear order. A totally ordered set is also called a chain.

Hasse Diagrams

We can represent a partial order graphically using a tool called a Hasse diagram. The idea is to draw the relation as a graph consisting of a vertex for every element in the set and edges denote which elements of the set are related by the partial order. For the sake of conciseness, edges which must appear (because of reflexivity and transitivity) are omitted.

For example, consider the poset $(\{1,2,3,4\}, \le)$. We start with all information.

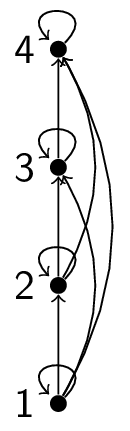
We now remove all self-loops:

We then remove the edges required for transitivity:

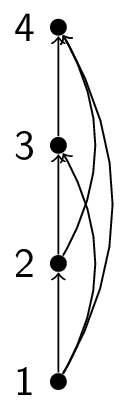
We now remove the arrows by placing all of the initial elements below the terminal elements:

This is the Hasse diagram.

Here are some more examples of Hasse diagrams:

• $(\{1,2,3,4,6,8,12\},|)$

  

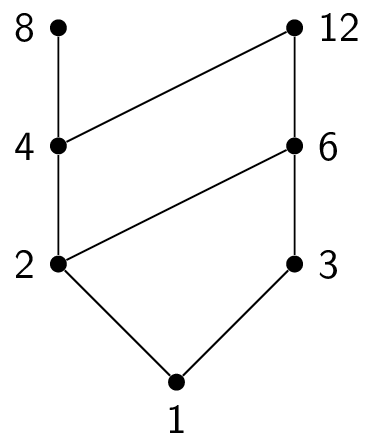
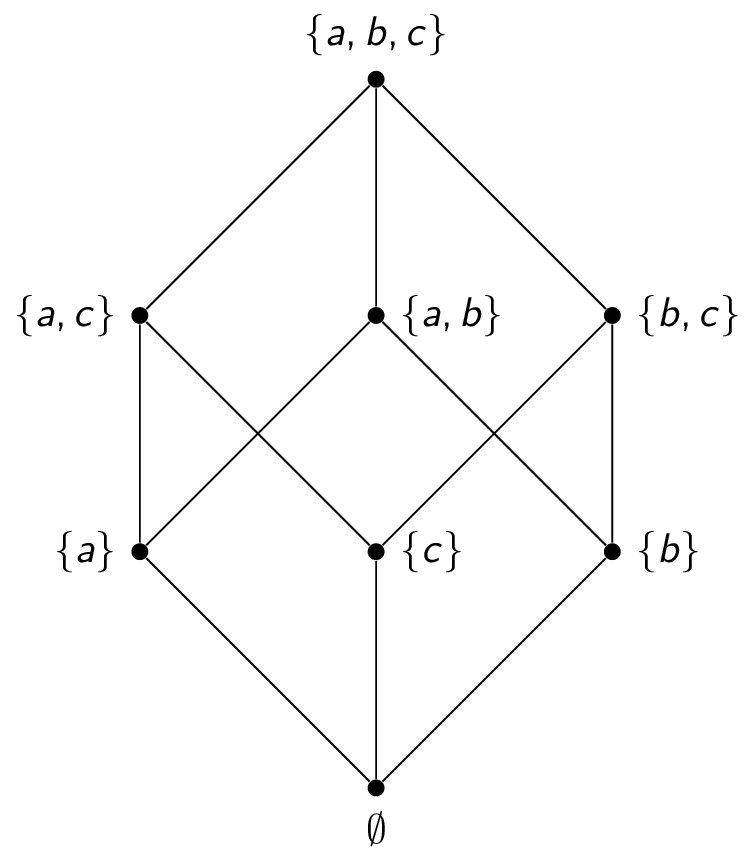
• $(\mathcal{P}{\{a,b,c\}}, \subseteq)$

  

The other benefit of Hasse diagrams is that it is easier to pick out certain special elements.

An element $a$ is maximal in a poset $(S,\preceq)$ if there is no $b \in S$ with $a \prec b$ (that is, $a \preceq b$ but $a \neq b$).

An element $a$ is minimal in a poset $(S,\preceq)$ if there is no $b \in S$ with $b \prec a$.

In a Hasse diagram, the maximal element(s) are at the top and the minimal element(s) are at the bottom, but only in the sense of where the edges enter and leave, not their location on the diagram!

• $(\{1,2,3,4,6,8,12\},|)$: $8,12$ are maximal, $1$ is minimal
• $(\mathcal{P}{\{a,b,c\}}, \subseteq)$: $\{a,b,c\}$ is maximal, $\emptyset$ is minimal

Sometimes, there is an element greater than every other element. If $b \preceq a$ for all $b \in S$, then $a$ is the greatest element of $(S,\preceq)$. If $a \preceq b$ for all $b \in S$, then $a$ is the least element of $(S,\preceq)$. Both the greatest and least elements are unique when they exist.

• $(\{1,2,3,4,6,8,12\},|)$: $1$ is the least element, but there is no greatest element
• $(\mathcal{P}{\{a,b,c\}}, \subseteq)$: $\{a,b,c\}$ is the greatest element, $\emptyset$ is the least element

You might want to bound some subset of the poset. Given a poset $(S,\preceq)$ and a subset $A \subseteq S$:

• if $u \in S$ and $a \preceq u$ for all $a \in A$, then $u$ is a upper bound of $A$
• if $l \in S$ and $l \preceq a$ for all $a \in A$, then $l$ is a lower bound of $A$

For example:

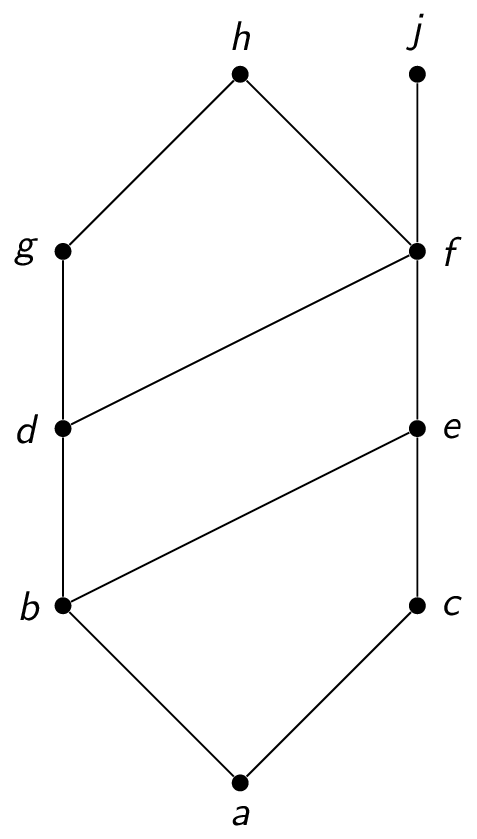
• upper bounds of $\{a,b,c\}$: $e,f,j,h$
• lower bounds of $\{a,b,c\}$: $a$
• upper bounds of $\{j,h\}$: none
• lower bounds of $\{j,h\}$: $a,b,c,d,e,f$
• upper bounds of $\{a,c,d,f\}$: $f,h,j$
• lower bounds of $\{a,c,d,f\}$: $a$

If $a \preceq x$ for any $a \in A$ and $x \preceq z$ for any upper bound $z$ of $A$ then $a$ is the least upper bound of $A$.

If $y$ is a lower bound of $A$ and $z \preceq y$ whenever $z$ is a lower bound of $A$ then $y$ is the greatest lower bound of $A$.

If the least upper bound or greatest lower bound exist, then they are unique.

In the previous example:

• the upper bounds of $\{b,d,g\}$ are $g,h$ and the least upper bound is $g$
• the lower bounds of $\{b,d,g\}$ are $a,b$ and the greatest lower bound is $b$

Topological Sorting

Suppose you are building a house. We can define a partial order on the "must be done before" relation: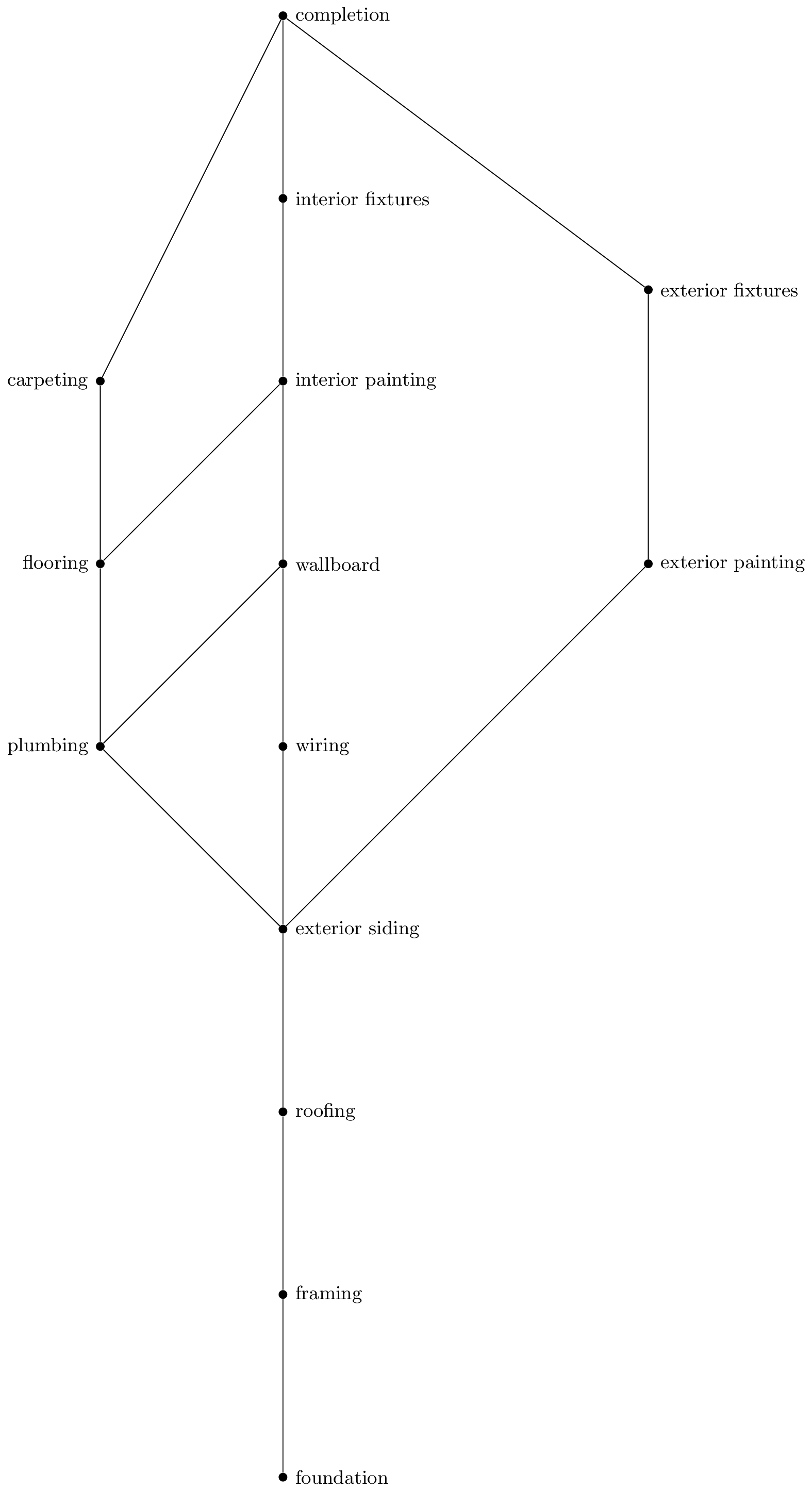

This is a partial order and must be respected when constructing a house. But this does not specify a valid ordering. There could be many! For example, we don't care if we do exterior painting or plumbing first (since they are incomparable elements).

We need a total order that respects the partial order. A total ordering $\preceq$ is compatible with a partial ordering $R$ if $a \preceq b$ whenever $aRb$.

Observe that every finite, non-empty poset has at least one minimal element.

Therefore, to find a compatible ordering, remove a minimal element and place it at the front of the total order. Now the initial partial order is a partial order with one fewer element. Keep doing this until all elements are gone. This is called topological sorting.

Here is how to topologically sort the poset $(\{1,2,3,4,6,8,12\},|)$. Here is the initial Hasse diagram:

The minimal element is $1$, which is the first element of our total order. This leaves us with the following Hasse diagram:

Both $2$ and $3$ are minimal elements, so we can select either. Let's pick $3$, which will be the second element in our total order. This leaves us with the following Hasse diagram:

$2$ is now the minimal element, which will be the third element in our total order. This leaves us with the following Hasse diagram:

Both $4$ and $6$ are minimal elements, so we can select either. Let's pick $4$, which will be the fourth element in our total order. This leaves us with the following Hasse diagram:

Both $6$ and $8$ are minimal elements, so we can select either. Let's pick $8$, which will be the fifth element in our total order. This leaves us with the following Hasse diagram:

$6$ is now the minimal element, which will be the sixth element in our total order. This leaves us with the following Hasse diagram:

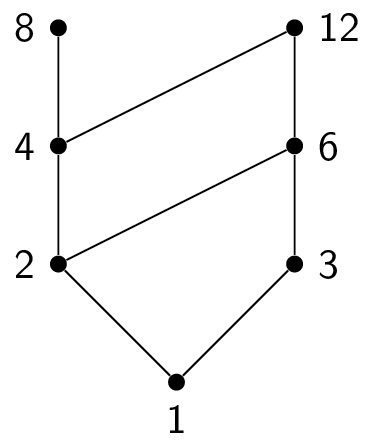
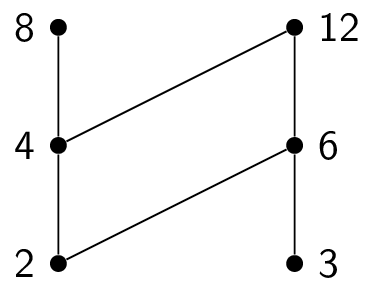
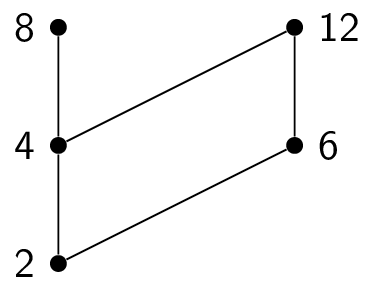
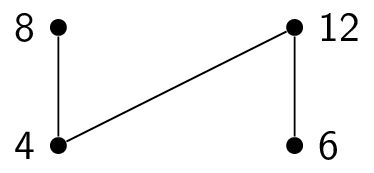
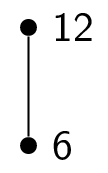
This means that the final element in the total order is $12$, giving us a total order of $1,3,2,4,8,6,12$. Other answers are possible!

A total order for house construction would be (for example) foundation, framing, roofing, exterior siding, plumbing, wiring, exterior painting, exterior fixtures, wallboard, flooring, interior painting, carpeting, interior fixtures, completion.