| COMP1406/1006 - Design and
Implementation of Computer Applications |
Winter 2006 |
What's in This Set of Notes?
We will not take a short break from GUI design and look at an important
programming style/technique known as Recursion.
In nature
(and
in mathematics), many problems are more easily represented (or
described)
using the notion of recursion. It is often the case that we
program
recursively so as to provide a simpler and more understandable solution
to
the problem being implemented. In fact, many data
structures
used in computer science are inherently recursive, making recursive
programming
natural and often efficient.
Here are the individual topics found in this
set of notes (click on one to go there):
One of the most common
techniques used in computer science is known as "divide and conquer".
This technique represents a strategy of dividing a complex
problem into smaller, easier-to-solve sub problems. There are
many real-world examples of how we break problems into smaller ones to
solve them:
- Jigsaw puzzles are solved in "steps": border, interesting
portion, grass, sky, etc..
- Math problems are broken down into smaller/simpler problems
- Even climbing stairs eventually breaks down to climbing one step
at a time.


So then what does this have to do with recursion ? Well,
recursion applies the divide and conquer strategy. The word Recursion actually
comes from a Latin word meaning "a running back". This
makes sense because recursion is the process of actually "going off"
and breaking down a problem into small pieces and then bringing the
solutions to those smaller pieces back together to form the complete
solution. Here are some points to remember:
- recursion breaks
down a complex problem into smaller
sub-problems
- subproblems are smaller
instances of the same
type of problem.
It sounds a little bit abstract doesn't it ? Why would we
want to do this anyway ?
- some problems are naturally
recursive
- e.g., especially math problems/functions such as factorial
- simpler, more
elegant solutions are often obtained
- easier
to understand completed solutions
- can be only
way to approach a seemingly overwhelming
problem
Do we really need recursion ? Well, any problem that is solved
recursively can also be done without recursion, but usually the
solution is more complex and it is difficult to consider all special
cases.
So, recursion is all about:
- figuring out how to break the problem down into smaller
sub-problems
- handling the smaller sub-problems
- figuring out how to merge the results of the smaller
sub-problems to answer the original problem
In fact, its actually easier than this sounds. Most of the
time, we
simply take the original problem and break/bite off a small piece that
we can work with. We simply keep biting off the small pieces of
the
problem, solve them, and then merge the results.
|

|
It is important to remember
the following very important facts about the sub-problems:
- must be an instance of the same
kind of problem
- must be smaller
than the original problem
|

|
So how many items do we bit off the small pieces ? When do
we know when to stop ?
Its simple. We stop when there are no more pieces ... or when the
remaining piece is so simple, that it is easily solved without needing
to break it down any further. At this "lowest level", we call
this simplest problem the "base case" or "basis case".
In fact, when writing the code, we usually start with the base cases
since they are the ones that we know how to handle. For
example, if we think of our "real world" examples mentioned earlier,
here are the base cases:
- For the jigsaw puzzle, we divide up the pieces until we
have just
a few (maybe 5 to 10) pieces that form an interesting part of our
picture. We stop dividing at that time and simply solve (by
putting
together) the simple base case problem of this small
sub picture. So
the base case is the problem where there are only a few pieces all
matching together.
- For the math problem, we simply keep breaking down the
problem
until either a) there is a simple expression remaining (e.g., 2 + 3) or
b) until we have a single number with no operations (e.g.,
7). These
are simple base cases in which there is either one operation to do or
none.
- For the stair climbing problem, our base case is our
simplest
case ... when there is only one stair. We simply climb that
stair.
|

|
Tips for Designing
Recursive Methods:
- Decide on a name for the method and
what its parameters
should be; you have to do this for non-recursive
methods just as well.
- You must believe
that the method
will work before you even begin to
implement
it; this is important. Without
it, you will not have
the faith to use the method to solve a simple problem especially if the
method isn't finished.
- You must decide on the simple
cases
that can be implemented trivially (the basis cases) and then write the
code.
- Determine a technique for breaking
up the more complicated case into simpler parts, some of which can be
done by using the original method with simpler parameters. This
is usually the hard part. Don't
think about the recursion. Just think about how to
express the original problem in terms of the smaller one's solution.
|

|
It would be a good idea to read the above tips again after you have
tried writing a couple of recursive methods.
5.2 Recursion With
Primitives
|
We now need to start looking at some examples of using
recursion. We will first consider examples in which the recursion
occurs without needing to manipulate any objects. That is,
we will look at a couple of examples in which recursion is used to
compute some values. The simplest example is that of using
the factorial function. In fact, the factorial example is
the "hello world" example of
recursion since the factorial function is a very
natural and simple operation that is inherently recursive.
By now, most of you know what the factorial operation does:
5! = 5*4*3*2*1
4! = 4*3*2*1
3! = 3*2*1
2! = 2*1
1! = 1
0! = 1
The operation is defined non-recursively as follows:
1
if N = 1
N! =
N x (N-1) x (N-2) x ... 3 x 2 x
1 if N > 1
We can easily write a factorial()
method that takes an integer and
computes the factorial using loops.
// A
non-recursive method for computing the factorial
public static int factorial(int
num) {
int result
= 1;
for (int
i=2; i<=num; i++)
result *= i;
return result;
}
How could we write this code recursively ? First, we must figure
out how to express the problem recursively. In this case it is
easy since there is a well-known recursive
definition:
1
if N = 1
N! = N x (N-1)!
if N > 1
Notice here that N! is defined in terms of
a smaller factorial problem ... that of (N-1)!. So we in fact
reduce our initial number N by 1. Then how do we solve the
(N-1)! problem ? Well, just apply the same formula:
(N-1)!
=
(N-1) x
((N-1)-1)! =
(N-1) x
(N-2)!
So then we need to break down (N-2)! ... which is done in the same
way. Eventually, as we keep reducing N by 1 each time, we end up with N=1 and for that simple problem we
know the answer is 1. So breaking it all down we see the
solution of 5! as follows:
So how do we write the code ? Its
easy. You start with the base case. Then use
the formula to break down the problem:
public static int
factorial(int
n) {
if
(n == 1) // BASE CASE
return
1;
return n * factorial(n - 1);
// RECURSIVE STEP
}
Wow! That's a simpler solution than
the non-recursive version. Did you notice how the method
actually calls itself ?
Recursive methods actually work just like your
"normal everyday" methods. There is nothing tricky. In
essence, each
time a message
is sent, a new "copy" of the method runs on a new copy of the
parameters. The local variables of one method invocation are not
visible
to another invocation.
Consider tracing the recursive execution of "2
factorial":
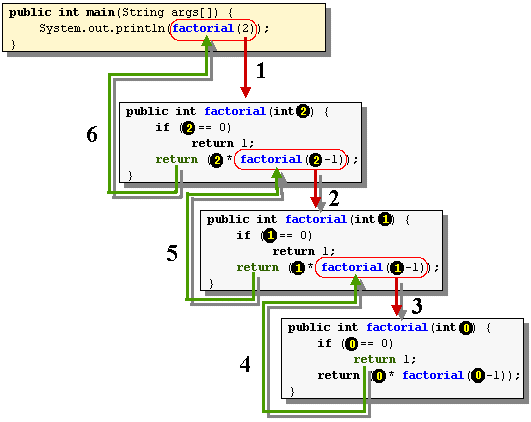
Below is the code as a test application. In it, we will make use
of
something new called command-line arguments.
Command-line arguments:
- are specified when running a JAVA program
- provide some additional information similar to the notion of
parameters.
- are passed as String parameters to the main method,
stored
in String args[].
- we can ask args for its length to see if there
are any command line arguments.
- you may not use spaces in your String parameters since a space
character is used to separate the parameters.
In JCreator, we can set the command line arguments by going to the Configure/Options menu and selecting JDK Tools. Than select the tool type to be Run Application. Select Default, then press Edit. Click on the Parameters tab and then select the
option "Prompt for main method arguments". Press
OK twice and then run your application. Now when you run,
you will be asked to enter some text for your application:
We will run our code the first time with the value of 5 as the command
line argument. So type 5 into the text field.
You should get a result of 120. Here is the code:
public class FactorialTest {
public static int factorial(int
n) {
if
(n == 1)
// BASE
CASE
return
1;
return n
* factorial(n
- 1);
//
RECURSIVE STEP
}
public static void main(String[] args) {
//First
check to see that there is at least one command line argument
if
(args.length
== 0) {
System.out.println("Usage: FactorialTest
anInteger");
System.exit(-1);
}
int theInteger
= Integer.parseInt(args[0]);
if
(theInteger < 0) {
System.out.println("Factorial of a negative int
is
not defined");
System.exit(-1);
}
else
System.out.println("Factorial of " +
theInteger + " is " + factorial(theInteger));
}
}
Did you notice how we can check the length of the args array to ensure that there is
at least one argument ? We then accessed that argument by
accessing the String array args
at its first position (which is the first parameter, which was the
number 5 we entered). Be aware though that the value comes
in as a String, so we have to parse it into the desired type.
What important test cases are not covered by
the code above ? Try entering 16, 17,
100. Are there any problems ? Do you know why ?
Example (Mortgage Payment Calculator):
Consider a
second recursion example that computes
how much money per month a person would have to pay to pay back a
mortgage on his/her home. Consider the following notation:
- p = the principal cost/amount of the home (e.g., $130,000)
- i
= the annual interest rate as a percentage (e.g., 3.5%)
- t
= the term (in months) that we wish the mortgage to be for (e.g., 300
months for a 25 year mortgage)
- m(p, i,
t) = the monthly payments we need to make based on the
parameters just mentioned (e.g., $647.57)
|

|
We would like to determine the value for m. Let us assume that t > 0, otherwise the point of
calculating a payment is silly anyway.
Certainly if the t = 1 then we
must pay one month interest and so the value of m should be p*(1+i) ... that is ... one month of
interest. Otherwise, we will consider the following recursive
formula to calculate the amount to be paid each month:
Now there are more accurate and efficient wasy to compute mortgage
payments, but we will use the above formula so that we can practice our
recursion.
So how do we write the code to do this ? Certainly the
function we need to write requires 3 parameters:
public static double
calculatePayment(int p, double i, int t) {
...
}
Now let us determine the base
case. It actually follows right
from the definition.
if (t
== 1)
return p*(1+i);
That wasn't so bad. Now what
about the recursive part ? It also follows from the formula:
return p / ((p / calculatePayment(p,i,t-1)) +
(1/Math.pow(1+i, t)));
So here is the whole thing:
public static double calculatePayment(int p, double i, int t) {
if (t == 1)
return p*(1+i);
return p / ((p / calculatePayment(p,i,t-1)) +
(1/Math.pow(1+i, t)));
}
Does it work ? We should write a test method.
Here is a class with our method, along with a main method that reads
the command line arguments:
public class MortgagePaymentCalculator {
public static double
calculatePayment(int p, double i, int t) {
if (t == 1)
return p*(1+i);
return p /
((p / calculatePayment(p,i,t-1)) + (1/Math.pow(1+i, t)));
}
public static void main(String[]
args) {
//First check to see that there is
at least three command line arguments
if (args.length < 3) {
System.out.println("Usage: MortgagePaymentCalculator principal interest rate term");
System.exit(-1);
}
int principal =
Integer.parseInt(args[0]);
double intRate =
Double.parseDouble(args[1]);
int term =
Integer.parseInt(args[2]);
System.out.printf("The monthly
mortgage payment for a %d month mortgage of $%,d " +
"home
at %1.3f percent annual interest is $%4.2f per month.",
term, principal, intRate,
calculatePayment(principal, intRate/100.0/12.0, term));
}
}
Notice that the user enters the interest rate as an annual rate (e.g.,
3.5) and the term is in months. We then need to adjust the
interest rate to be a percentage (hence divide by 100) and also to make
it monthly to match the term units (hence divide by 12).
So from our two examples, you can see that recursion is quite simple
once you have a recursive formula.
5.3 Recursion With
Objects (Non-Destructive)
|
Now that we have seen some simple
examples of recursion that dealt only with some primitive calculations,
we need to look at how recursion works when objects are
involved. Let us look at a simple example of reversing a
string.
Example (Reversing a
String):
As you may
know, strings in JAVA are not mutatable
(that is, you cannot actually modify a string once it is
made). We
will look at a method that takes a string and then returns a new string
which has the same characters as the original, but in reverse order:
public static
String reverse(String
s) {
...
}
|

|
We start by considering the base case. What strings are
the easiest ones to solve this problem for ? Well, a string
with 1 or 0 characters is easy, since there is no reversing to
do. So there you have it. Those are the base
cases:
if (s.length()
== 1)
return s;
if (s.length()
== 0)
return s;
We can simplify this to one line:
if (s.length() <= 1) return
s;
Now, how do we express the problem recursively ?
Remember ... think of a smaller problem of the same type. A
smaller problem would be a smaller string. So what if we
take a piece of the string and then solve for the smaller string
? That is the way we should approach it. What
piece should we take off ? Perhaps the first
character. We can use:
s.substring(1,
s.length())
to get the smaller string which is the original without the first
character.
OK. Now what do we do ? Remember, we need to
express the solution to original problem in terms of the smaller
problem. So we should be thinking the following question:
"If I have the reverse of the smaller string, how can I use that to
determine the reverse of the whole string ?". Lets look at
an example:
"STRING" reversed is "GNIRTS". If we use consider the
shorter string "TRING" and reverse it to "GNIRT", then how can we use
this reversed shorter string "GNIRT" to obtain the solution "GNIRTS" to
the original problem ? You can see that all we have to do
is append the "S" to the smaller string solution "GNIRT" to get the
complete solution "GNIRTS". So,
reverse("STRING") = reverse("TRING") + "S"
Now we should know how to write the code:
public static String reverse(String s) {
if
(s.length() <= 1) return s;
return reverse(s.substring(1,
s.length())) + s.charAt(0);
}
As you can see the solution is quite simple ... after we see the solution of course
;).
Here is the test code:
public class ReverseTest {
public
static String reverse(String s) {
if
(s.length()
<= 1) return s;
return reverse(s.substring(1, s.length())) +
s.charAt(0);
}
public static
void main(String[] args) {
//First
check to see that there is at least one command line argument
if (args.length
== 0) {
System.out.println("Usage: ReverseTest
aString");
System.exit(-1);
}
System.out.println(args[0] + " reversed is "
+ reverse(args[0]));
}
}
Example (Palindromes):
Consider the simple problem of
determining
whether or not a String is a palindrome. A palindrome is
a String which reads the same forwards
as backwards:
How do we write a method using a for loop to
detect whether or not a String is a palindrome ? Well ...
how
do we do it without a computer ? |

|
We probably compare the
first and last characters and then work our way inward toward the
center of the String:
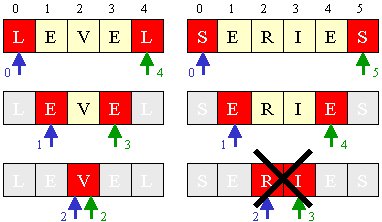
Here is how we may write code to do this:
public static boolean isPalindrome(String s) {
for (int i=0;
i<=(s.length()-1)/2; i++) {
if (s.charAt(i)
!= s.charAt(s.length() - i - 1))
return false;
}
return true;
}
Now what about solving this recursively ?
We must be able to express the palindrome problem in terms of
smaller
palindrome problems.
Here is the recursive formulation of the problem:
- A String is a palindrome if its first and last characters are
identical AND the substring in between is a palindrome.
Here is how the recursion can be done:
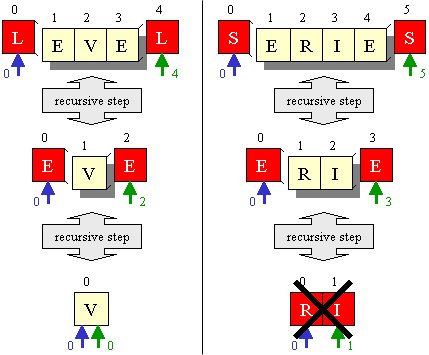
For example, in our palindrome problem, when only 1 character
remains
in the String, or in the case where the String is empty, we don't need
to
divide any further and so these are the base cases for our
problem.
Often, the base cases also correspond similarly with error-checking
(e.g.,
like checking for an empty string first). So ... the base
case is used to "stop" the recursive process.
Here are some palindrome examples that show when the base case is
reached.
isPalindrome("level")
---> isPalindrome("eve")
---> isPalindrome("v")
---> true
isPalindrome("poop") ---> isPalindrome("oo") ---> isPalindrome("") ---> true
isPalindrome("abcdba") --->
isPalindrome("bcdb") --->
isPalindrome("cd") ---> false
So how do we write the code for this problem recursively
? Think of the stopping conditions and write pseudo code:
- if the string is empty return true (i.e.,
an
empty string is considered a palindrome)
- if the string has only 1 character in it, return true
- otherwise ... if the first and last characters do not match,
return false
- otherwise return the result of the recursive sub-problem
on a substring which excludes the first and last characters
Start the code with the base cases, then do the recursive part:
public class StringUtilities
{
public static boolean
isPalindrome(String s) {
//BASE CASE (1 or 0 character cases combined together here)
if (s.length()
<= 1)
return true;
//BASE CASE (first and last characters do not match)
if
(s.charAt(0) != s.charAt(s.length() - 1) )
return
false;
//RECURSIVE STEP (check if middle portion is a palindrome)
return
isPalindrome(s.substring(1,
(s.length() - 1)));
}
}
Here is another way to write it:
public static boolean isPalindrome(String s) {
return ((s.length()
<= 1) ||
((s.charAt(0) == s.charAt(s.length() -
1)) &&
(isPalindrome(s.substring(1, (s.length() -
1))))));
}
Now we must write a test application. Here is some testing code
written in a different class:
public class PalindromeTest
{
public static void main(String[] args) {
//First
check to see that there is at least one command line argument
if
(args.length
== 0) {
System.out.println("Usage: PalindromeTest
aString");
System.exit(-1);
}
String input =
args[0]; // Access the first argument from the
argument list
if
(StringUtilities.isPalindrome(input))
System.out.println(input + " is a palindrome ");
else
System.out.println(input + " is NOT a palindrome
" );
}
}
| 5.4 Recursion With Objects (Destructive) |
In the previous section, we
showed how we could break pieces off of Strings each time we called the
method recursively. In fact, we did not really alter the
string, since the substring()
method actually returns a new string. As a result, we did
not really destroy the original string. Sometimes,
however we might want to use a destructive
modification of an object. For example we might want the actual
elements of an object to be altered, instead of making a new object
that represents the changes to the original.
- Destructive methods - alter
the receiver or parameters in some way to obtain result.
- Non-destructive methods -
usually creates new objects to contain the "answer" to the problem,
leaving the
receiver and/or parameters intact.
Often, it is easier to destroy an object when
performing an operation. For example, if someone asked you to
count the jelly
beans in a big jar you would probably not leave the jar intact.
Instead,
you'd alter it by removing the jelly beans one at a time (or in small
amounts)
and do the counting while placing the counted jelly beans in a new and
initially empty jar (or eating them !). To do this
completely non-destructively, you'd have to count the beans without
taking them out of the jar....a difficult task indeed.

In the case where the object is temporarily destroyed during the
computation and then restored at the end, this is considered to
be Non-Destructive. For instance, we may
temporarily remove the jelly beans from the jar to
count them and then put them back in when done. From the
outsiders
point of view, the jar arrangement has not been destroyed. We do
realize however that the order of the jelly beans has been
altered. If the order was important, then this process is
considered destructive, as we
are destroying the ordering.
Another approach that is common is to take the
original object, make a copy and then write a destructive
method on the copy. This is kind of like "cheating" but it does
solve the problem, of course
with the added running time overhead of copying the original object
beforehand. This often leads to the need to write more than one
method (i.e., use helper methods) to solve the problem. We will
see later
that this brings up the notion of indirect recursion.
The notion of writing destructive or non-destructive methods is not
something specific to recursion. In fact, you have already
written some destructive AND non-destructive methods in
COMP1405/1005.
Example (Summing
Elements in an ArrayList)
Assume that we have an
ArrayList of Integer
objects. Consider writing a function that sums the integers
in the ArrayList:
public static int
sum(ArrayList<Integer>
anArrayList) {
int sum=0;
for(Integer x: anArrayList)
sum += x;
return sum;
}
|

|
As you can see, we simply go through the elements one by one and
compute the total:
What about doing it recursively ? How
do we define the problem recursively ?
We can do this as follows:
- grab the first element and add it to
the sum
- remove it from the ArrayList and
recursively sum the remaining Integers.
Note this strategy is destructive
in that it modifies the ArrayList by removing all of its components.
Nevertheless, let us examine how this is done.
First, we consider the recursion by finding
the simple base cases:
- if the ArrayList is empty, then
the sum is 0
- if the ArrayList
has only one element,
then the sum is that element
- otherwise we must do some recursion
Here is the code:
public static int
sum(ArrayList<Integer>
arrayList) {
//BASE CASES
if
(arrayList.isEmpty())
return
0;
if
(arrayList.size() == 1)
return
arrayList.get(0);
//RECURSIVE STEP
Integer element = arrayList.get(0);
arrayList.remove(element);
return
element.intValue() + sum(arrayList);
}
|
 |
But wait. Think about what happens as we
empty elements from the ArrayList and head towards the base case.
Do we really need that second base case ? The
answer is NO since one more step of the recursive case will bring us to
the
first base case. Hence, we can simplify the code by removing the
second
base case:
public static int sum(ArrayList<Integer>
arrayList) {
if
(arrayList.isEmpty()) return
0;
Integer
element =
arrayList.get(0);
arrayList.remove(element);
return
element.intValue() + sum(arrayList);
}
This hardly seems more efficient than the non-recursive
version!! As mentioned before, some problems are not meant to be
done recursively. We are simply examining them recursively
for practice in order to help us understand recursion.
In some cases, the recursive solution is
simpler. Consider summing Integer
objects that are in a
Stack:
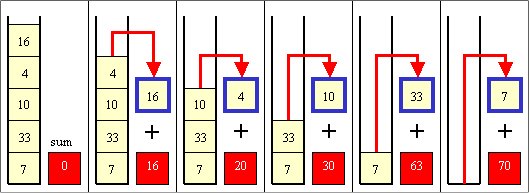
public static int sum(Stack<Integer>
s) {
int sum=0;
while(!s.isEmpty())
sum += s.pop();
return sum;
}
Is this destructive ? Yes!
What
does the recursive version look like ?
- The sum(s)
= firstElementOf(s) + sum(s
without the first element)
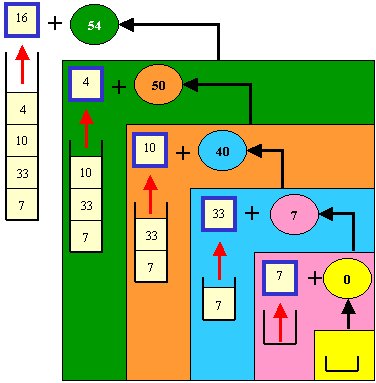
Here is the code:
public static int sum(Stack<Integer>
s) {
if (s.isEmpty())
return 0;
return
s.pop() + sum(s);
}
It is roughly the same amount of
code.
But now, what if we wanted to write these methods non-destructively ?
We need to put the items back onto the Stack so that
the Stack is restored.
Here is the non-recursive, non-destructive version:
public static int sum(Stack<Integer>
s) {
int sum=0;
Stack<Integer> tempStack = new
Stack<Integer>();
while(!s.isEmpty()) {
Integer item = s.pop();
sum += item;
tempStack.push(item); // Keep backup of popped items
}
//Restore the original
Stack
while(!tempStack.isEmpty()) {
s.push(tempStack.pop());
}
return sum;
}
Notice that we had to write code to keep track of
the items that we removed so that we could put them back
later.
We used another Stack to keep
this information, but we could have used
any
kind of collection.
Now what about the non-destructive recursive
version ?
public static int sum(Stack<Integer>
s) {
if (s.isEmpty())
return 0;
Integer element =
s.pop(); // temporarily
destroy stack
int answer =
element + sum(s); // get recursive sum
s.push(element);
// restore after the recursion
return answer;
}
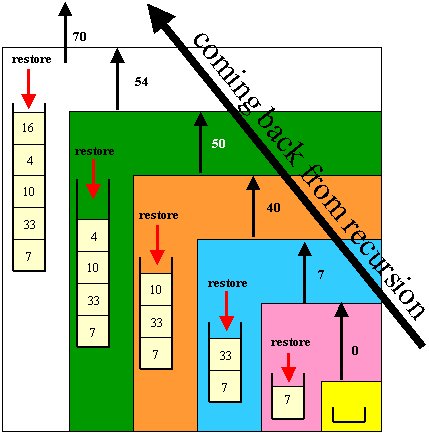
Hey! It is much simpler. We don't need extra
variables. We simply restore the popped item on the way
back from the recursion. This is an example of temporarily
destroying the object in order to get
an answer and then "undo"ing the destroying on the way back from the
recursion. It is considered a non-destructive method.
So we can see that the recursive solution is more elegant.
Example (Counting):
Consider
counting the elements in some kind of
collection. Perhaps we want to only count elements that satisfy
some condition. In this example, we count the odd integers in an
ArrayList. We
will do it first destructively, and then
alter our code to make it non-destructive.
Destructively, we can simply take off one element from the ArrayList
each time through the recursion. We simply look at the number
that we take out and add one to the total each time it is found to be
odd.
|

|
Here is the destructive version inside a text
class:
import java.io.*;
import
java.util.*;
public
class CountTest {
public static int countOdd(ArrayList<Integer>
nums) {
//BASE CASE
if (nums.isEmpty()) return 0;
//RECURSIVE STEP
Integer element = nums.get(0);
nums.remove(element);
if (element%2 == 0)
return countOdd(nums);
else
return 1 + countOdd(nums);
}
public static void main(String[]
args){
int input
= 0;
ArrayList<Integer> nums = new ArrayList<Integer>();
do {
System.out.println("Enter integers one at a time (0 to
end):");
if ((input
= new Scanner(System.in).nextInt())
!= 0)
nums.add(input);
} while (input != 0);
System.out.println("There were "
+ countOdd(nums) + " odd
integers entered.");
}
}
How can we do it non-destructively ? We need to ensure that
anything we remove is put back in on the way back from the
recursion. Since we begin by removing the first element
from the ArrayList and then doing the recursion, we must add that
removed element back to the front of the ArrayList AFTER the recursion
is done. If we do this at every step, the ArrayList should
be back to normal. Notice the changes that we need to make:
public static int countOdd(ArrayList<Integer>
nums) {
//BASE CASE
if (nums.isEmpty()) return 0;
//RECURSIVE STEP
Integer element = nums.get(0);
nums.remove(element);
int result = 0;
if (element%2 == 0)
result = countOdd(nums);
else
result = 1 + countOdd(nums);
// Add the element
back to the collection before returning
nums.add(0, element);
return result;
|
}
In fact, we can simplify this code further, noticing that both
conditions in the IF statement
call recursively:
public static int countOdd(ArrayList<Integer>
nums) {
//BASE CASE
if (nums.isEmpty()) return 0;
//RECURSIVE STEP
Integer element = nums.get(0);
nums.remove(element);
int
result = countOdd(nums);
if (element%2 != 0) result++;
// Add the element back to the
collection before returning
nums.add(0, element);
return
result;
}
| 5.5 Direct vs. Indirect
Recursion |
A method that calls a recursive method is considered recursive
itself. If the method calls itself, it is considered to be directly
recursive. In general, it is possible for two or
more methods to call one another repeatedly. This is
commonly termed "mutual"
recursion. For example, method
A
calls method B, which calls method A again
etc...
We use the term "indirect"
recursion to describe a method
which itself is not recursive, but which calls a directly recursive
method to
compute its solution. The isPalindrome() method
that we
wrote is considered directly recursive as it calls itself
recursively.
|
Example (Summing Integers in an
Array)
Let us look again at the example of summing integers, but this
time
using an array of ints. We cannot remove from the array as we did
with the ArrayLists and Stacks in the previous section of
the
notes. We must take a different, non-destructive,
approach. How would we do this non-recursively ?
public static int
sum(int[]
theArray) {
int result
= 0;
for (int
i=0; i<theArray.length; i++)
result += theArray[i];
return
result;
}
|
 |
Now this is non-destructive because
it merely accesses the array elements without removing or changing them.
How can we do this recursively ? At each
step of the recursion, we will need to know which number we are adding,
so
we will
also need an index. Where do we put this index ? It MUST
be
a parameter to the method so that this position needs to be carried
through the recursive iterations:
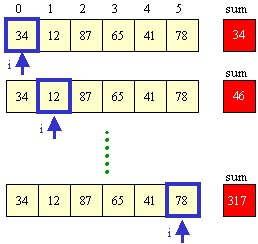
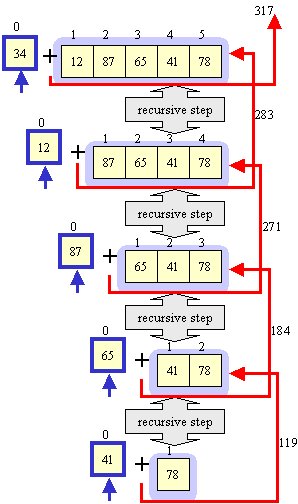
private static int sum(int[] theArray, int n) {
//BASE
CASE: sum(theArray,0) = a[0]
if (n == 0) return
theArray[0];
//RECURSIVE
STEP: sum(theArray,n) = theArray[n] + sum(theArray,n-1)
return
(theArray[n] + sum(theArray,n-1));
}
Notice that this method adds the elements in
reverse order. That is different from the non-recursive
method. It is more natural this way since we continually reduce
the value of n until we
reach the base case of n == 0.
Note that we did not do any error checking. What if n is greater
than the
array length ?
We do have one annoying problem now ... we have
to
supply an additional parameter.
To avoid this problem, we will make another method
that will be called by the user in place of this one. This new
method
will provide the parameter for us:
public static int sum(int[] theArray) {
return (sum(theArray,
theArray.length - 1);
}
Can we have these two methods with the same name
? Yes ... since they have a different signature (i.e., parameter
list).
Recall that this is known as overloading.
Now to test it we merely call this new
method.
In fact, we should make the original method private. This technique of making a kind of "wrapper" for the
recursive method is known as indirect recursion.
The first
method is directly recursive but this second one is
called indirectly
recursive since it does not call itself, but does call a
recursive
method. This second method is commonly called a helper
method.
It should be a simple task for you to take the
ArrayList method that we wrote earlier and make it
non-destructive. Make sure you can do
this. Here is the code altogether:
//Example of summing elements of Arrays
and Arr using recursive and
overloaded
sum methods.
import java.io.*;
import java.util.*;
public class SumTest
{
//This destructive method
returns the sum of a vector of Integers
public static
int sum(ArrayList<Integer> arrayList) {
//BASE CASE
if (arrayList.isEmpty()) return 0;
//RECURSIVE STEP
Integer element =
arrayList.get(0);
arrayList.remove(element);
return (element.intValue() +
sum(arrayList));
}
//This is a helper
method
private static int sum(int[]
theArray, int n) {
if (n == 0) return
theArray[0];
return
(theArray[n] + sum(theArray,n-1));
}
//This method returns
the sum of an array of Integers .
public static int sum(int[] anArray) {
return (sum(anArray,
anArray.length-1));
}
public static void main(String[] args) throws IOException {
int MAX = 100,
i=0, count=0, temp=0;
int[] a = new
int[MAX];
ArrayList<Integer>
arrayList = new ArrayList<Integer>();
System.out.println("Enter the first integer (0 to end, Max=100):");
//Add
first number to array and vector
temp = new Scanner(System.in).nextInt();
a[i] = temp;
arrayList.add(new
Integer(temp));
//read
numbers into array and vector
while ((a[i] !=
0) && (i < MAX)) {
i++;
count++;
System.out.println("Enter another integer (0 to
end):");
temp = new Scanner(System.in).nextInt();
a[i]
= temp;
arrayList.add(new Integer(temp));
}
System.out.println("Here are the results:");
System.out.println("Array Sum = " + sum(a));
System.out.println("ArrayList Sum = " + sum(arrayList));
}
}
Note that this method adds the final zero to the arrayList and
the array. Can you fix this problem ? I hope
so.
Does it matter
?
Example
(Reversing a
StringBuffer):
Consider our earlier example in
which we reversed
the characters of a String.
We could replace the String with
a StringBuffer and then
change our method so that the actual characters of the
original StringBuffer would
be reversed. This would be considered a destructive method since
it modifies the original object parameters.
Take notice of the method overloading and the use of a private
helper method.
|

|
Our strategy will be to swap the first and last characters of the StringBuffer and then move inwards
on the StringBuffer the same
way we iterated through the String in
our palindrome example. To do this, we will not shrink the StringBuffer each time.
Instead, we will keep track of where we are by using indices as we
traverse recursively. We will write the following method
which will reverse the characters of the given StringBuffer within the indices
specified by i and j:
private static void
reverseBetween(StringBuffer s, int
leftIndex, int rightIndex) { ... }
We will call this method recursively, increasing leftIndex each time while
decreasing rightIndex.
Thus the base case will be the stopping condition when leftIndex is greater than or equal
to the rightIndex.
Here is the code:
private
static void reverseBetween(StringBuffer s, int leftIndex, int rightIndex) {
//BASE
CASE
if (leftIndex
>= rightIndex )return;
//RECURSIVE
STEP
char temp =
s.charAt(leftIndex);
s.setCharAt(leftIndex,
s.charAt(rightIndex));
s.setCharAt(rightIndex,
temp);
reverseBetween(s, leftIndex+1, rightIndex-1);
}
Notice that the
method does not return anything. It is simply a procedure
that modifies the argument passed to it (i.e., modifies the StringBuffer).
Of course, this is not the method that we wanted. We want
the following method signature:
public static void
reverse(StringBuffer s) { ... }
But we can make use of the reverseBetween()
method, just ensuring that we pass in "good" leftIndex and rightIndex parameters:
//Reverse the contents
of
StringBuffer s
public static void reverse(StringBuffer s) {
if (s.length()
> 1)
reverseBetween(s, 0, s.length()-1);
}
Notice that this method is "indirectly" recursive since it calls a
recursive method, but it does not call itself. Here is the
test code:
public class DReverseTest {
//Reverse the contents
of
StringBuffer s
public static void reverse(StringBuffer s) { ...
}
private
static void reverseBetween(StringBuffer
s, int leftIndex, int rightIndex)
{ ... }
public static void main(String[] args) {
//First
check to see that there is at least one command line argument
if (args.length
== 0) {
System.out.println("Usage: DReverseTest
aString");
System.exit(-1);
}
StringBuffer input = new
StringBuffer(args[0]);
System.out.println("string buffer's initial contents: " + input);
reverse(input); //Notice that we call the public method
System.out.println("string buffer's final contents: "
+ input);
}
}
| Example
(Averaging):
Consider finding the average of a set of
Integers that are stored in an ArrayList.
One approach is to
use the sum method just mentioned and merely divide by the
number of elements:
public
static double avg(ArrayList<Integer>
v) {
return (sum(v) / (double)v.size());
}
|
|
This approach is fine and will work as
desired. However, a more interesting challenge is to write a
recursive averaging
method, without using the sum()
method. Let us try to see if we can
express
the averaging function recursively. We will say that avg(A, n) is the function for finding the
average of n numbers stored in an ArrayList A. We
will
denote the elements of the ArrayList A to be A1, A2, A3, ..., An.
What about the base cases ?
avg(A, 0) = 0
avg(A, 1) = A1
Now the inductive case:
avg(A, n)
= (A1 + A2 + A3 + ... + An)
/ n
= [(A1 + A2+ A3 + ... + An-1) / n] + [An / n]
= [((n-1) / n) * (A1 + A2+ A3
+ ... + An-1) /(n-1)]
+ [An / n]
= [((n-1) / n) * avg(A,
n-1)] + [An
/ n]
= [((n-1) * avg(A,
n-1) + An
] / n
So the recursive definition is:
avg(A, 0) = 0
avg(A, 1) = A1
avg(A, n) = [((n-1)
* avg(A, n-1) + An
] / n
Now we can easily write the code:
import java.io.*;
import java.util.*;
public class AvgTest
{
//This method returns the
average of a n Integers in the given vector .
private static double avg(ArrayList<Integer>
a, int n) {
//BASE
CASES:
if (n > a.size()) return -1;
if (n == 0) return
0;
Integer last = a.get(a.size() - 1);
if (n == 1) return
last;
//RECURSIVE
STEP
a.remove(last);
return (((n-1) *
avg(a, n-1) +
last)/n);
}
//This method returns
the average of an ArrayList of Integers
public static double avg(ArrayList<Integer> a) {
return (avg(a, a.size()));
}
public static
void main(String[] args) {
int input = 0;
ArrayList<Integer> nums = new ArrayList<Integer>();
do {
System.out.println("Enter integers one at a time (0 to
end):");
if ((input
= new Scanner(System.in).nextInt())
!= 0)
nums.add(input);
} while (input != 0);
System.out.println("The average is " +
avg(nums));
}
}
Do we really need this extra index ? Can we re-write
this
method using direct recursion ? Well the index of n
represents the size of the array, which changes as the recursion
progresses. So we have to be careful:
private static double avg(ArrayList<Integer> a) {
if (a.isEmpty()) return 0;
Integer last = a.get(a.size() - 1);
if (a.size() == 1)
return
last;
a.remove(last);
int size = a.size();
return (size * avg(a) +
last)/(size+1);
}
Notice the use of the size variable
to that when the ArrayList size
changes due to the recursion, this local variable stays constant.
We can re-arrange the order of the calculations in the expression if we
want to eliminate this extra size variable.
We just have to
make sure that the size is
used BEFORE the recursive call:
private static double avg(ArrayList<Integer> a) {
if (vec.isEmpty()) return 0;
Integer last = a.get(a.size() - 1);
if (a.size() == 1)
return
last;
vec.remove(last);
return
(1/(a.size()+1.0))*(a.size()
* avg(a)
+ last);
}
Of course, we can play games like this all day long :). We
can actually eliminate the 2nd base case, since it is handled by the
recursive call:
private static double avg(ArrayList<Integer> a) {
if (a.isEmpty()) return 0;
Integer last = a.get(a.size() - 1);
a.remove(last);
return
(1/(a.size()+1.0))*(a.size()
* avg(a)
+ last);
}
Also, we can get rid of the last variable
by re-arranging the
expression again:
private static double avg(ArrayList<Integer> a) {
if (a.isEmpty()) return 0;
return
(1.0/(a.size()))*(a.remove(0) + a.size() *
avg(a));
}
But WHY would you write such a complicated looking expression
??? It is better to leave the last variable as it was for ease of
reading the code.
| Example
(Selecting):
Now, what if we wanted to not just count
the odd
integers in an ArrayList, but
to gather and return them (i.e., select them)
? That is, make a new ArrayList
that will contain all of the odd
integers from the original
ArrayList. Can we do this with direct recursion ? Perhaps
we
should
make a helper method.
We can take the approach that is common to
everyday life. Get a blank list ready, and write down all
the odd integers in it. In terms of coding, we can prepare
the blank "list" as an initially empty ArrayList passed in as a
parameter. We can then add to this list as we go through
the recursion. Hence we will need to pass this list along when we
do the recursive calls.
|

|
import java.io.*;
import java.util.*;
public class SelectTest {
//This destructive method returns the odd Integers in
an ArrayList
public static
ArrayList<Integer>
selectOdd(ArrayList<Integer> a) {
return
(selectOdd(a,
new ArrayList<Integer>()));
}
//This is the helper method that does all of the work
public static
ArrayList<Integer> selectOdd(ArrayList<Integer> a, ArrayList<Integer>
result) {
//BASE CASE:
if (a.isEmpty()) return result;
//RECURSIVE STEP
Integer element = a.get(0);
a.remove(element);
if (element%2 != 0)
result.add(element);
return selectOdd(a,
result);
}
public static
void main(String[] args) {
int input
= 0;
ArrayList<Integer> nums = new ArrayList<Integer>();
do {
System.out.println("Enter integers one at a time (0 to
end):");
if ((input
= new Scanner(System.in).nextInt())
!= 0)
nums.add(input);
} while (input != 0);
ArrayList<Integer> result = selectOdd(nums);
System.out.println("Here
are the odd
integers:");
for (int i=0; i<result.size(); i++) {
System.out.println(result.get(i));
}
}
}
Can you write this method using direct recursion (i.e., no
additional
parameters) ?
public static
ArrayList<Integer> selectOdd(ArrayList<Integer>
a) {
if (a.isEmpty())
return
new ArrayList<Integer>();
Integer element = a.get(0);
a.remove(element);
result = selectOdd(a);
if (element%2 != 0)
result.add(element);
return result;
}
Do the odd numbers come back in the same order as before
? Think about it.
What about making it non-destructive now:
public static
ArrayList<Integer> selectOdd(ArrayList<Integer>
a) {
if (a.isEmpty()) return new ArrayList<Integer>();
Integer element = a.get(0); //remove
from end now
a.remove(element);
result = selectOdd(a);
a.add(element); //restore after
recursive
call by adding to end
if (element%2 != 0)
result.add(element);
return result;
}
| Example
(Choosing k items from N):
Denote the number of ways of choosing k items out of N by
C(N,k). We can
determine what
this number is by doing an experiment and counting.
The approach we'll take is to look at any one
particular item, say X, and decide
if it is either going to be chosen in the answer or if it is not.
All possibilities have to be considered.
- If X
is chosen, there are N-1 items
left
from which we must still choose k-1
(one has already been chosen).
- If X
is not chosen, there are N-1 items left from which we still
must choose k (since we haven't
chosen any yet).
That is, C(N,k) =
C(N-1,k-1) + C(N-1,k)
|

|
We can define the degenerate cases (the basis) as
1. C(N,N) = 1
2. C(N,0) = 1
3. C(N,k) = 0
if k > N (We assume k <= N always)
Here is the code:
//Computing C(n,k) example. (use:
java ChooseTest n k)
public class ChooseTest {
//returns C(n,k)
public static int choose(int n, int k) {
//BASE CASES:
if (n == k) return
1; //C(n,n) = 1
if (k == 0) return
1; //C(n,0) = 1
if (k > n) return
0; //C(n,k) = 0
//RECURSIVE
CASES: C(N,k) = C(N-1,k-1) + C(N-1,k)
return (choose(n-1,k-1) + choose(n-1,k));
}
public static void main(String[] args) {
//First
check to see that there is at least one command line argument
if (args.length
< 2) {
System.out.println("Usage: ChooseTest n k");
System.exit(-1);
}
int n =
Integer.parseInt(args[0]);
int k =
Integer.parseInt(args[1]);
System.out.println("C(" + n + "," +
k + ")= " + choose(n,k));
}
}
Example
(Counting boxes
within boxes):
Consider the following scenario. You wrap
up
your friends graduation gift in a box...but to be funny, you decide to
wrap
that box in a box and that one in yet another box. Also, to
fool
him/her you throw additional wrapped boxes inside the main
box.
The boxes-within-boxes scenario is recursive. Consider this
problem
now. We have boxes that are completely contained within
other
boxes and we would like to count how many boxes are completely
contained
within
any given box. Here is an example where the outer box has
29
internal boxes:
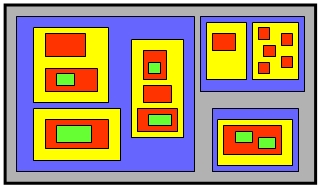
|

|
Assume that there are some classes that implement
the following Box interface:
public interface Box
{
public ArrayList<Box> internalBoxes(); //Returns
the boxes within the receiver box
public boolean isEmpty();
//Return whether or not there are any boxes
within
the receiver box
public void
addBox(Box
aBox); //Add the given
box to the receiver
public void
removeBox(Box
aBox); //Remove the given box from the
receiver
}
Now we have no idea how the boxes are stored or maintained.
All
we know is how to use the interface.
How can we write a recursive method to find the total number of boxes
with a given box ?
- Base case:
if the given box is empty, the answer is 0.
- Inductive case: the number of boxes
directly within the receiver + the total of the number of internal
boxes
within each box that is within the receiver.
Here is the code:
public int countBoxes(Box
aBox) {
if (aBox.isEmpty())
return 0;
int count = 0;
ArrayList<Box> innerBoxes =
aBox.internalBoxes();
// Go through each
internal box and get count
// their internal boxes
recursively
for (Box b: innerBoxes) {
count += countBoxes(b);
}
// Return the count of
all internal boxes' boxes plus the number
// of internal boxes at
this level of the recursion
return (count + innerBoxes.size());
}
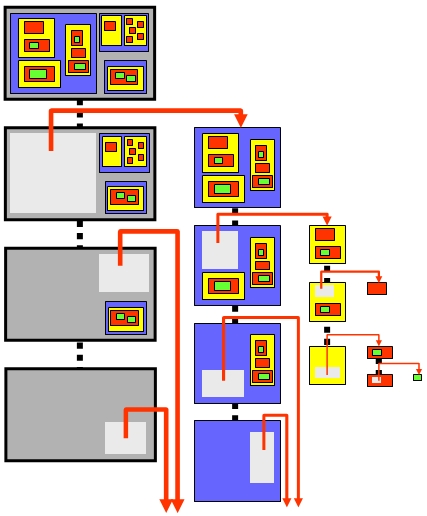
Notice that we need the for loop here to go through
all
internal boxes. What if we were allowed to destroy the boxes
?
Can we do this without a for loop ?
 =
= 
Here is the code:
public int countBoxes(Box
aBox) {
if (aBox.isEmpty())
return 0;
Box anInnerBox =
aBox.internalBoxes().get(0);
aBox.removeBox(anInnerBox);
return (countBoxes(aBox)
+ countBoxes(anInnerBox)
+ 1);
}
Will this work ? Think about it. Are the recursive sub
problems always smaller ? Which of the two pieces of code do you prefer
?
Try writing a class that implements the box interface and test this
method out.
Example
(Height of a Tree):
Consider a class called BinaryTree that
keeps a collection of nodes. The topmost node is
the root of the tree. Each node stores an item
of some kind and keeps pointers to a left and right child.
The children are themselves trees and are considered subtrees
of the original tree. If a node has no left or right child,
then null
is stored there. A node with no children at all is considered a leaf.
|

|
Here is an example of a binary tree:
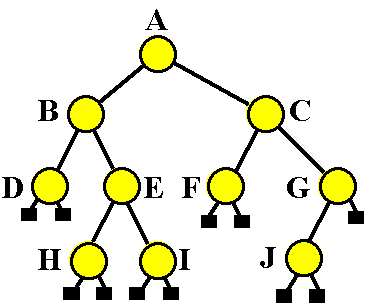
A basic implementation of a binary tree may look
like this:
public class TreeNode {
private TreeNode rightChild,
leftChild;
private Object
item; // set to whatever the node
represents
public TreeNode(Object
anObject) {
this(anObject, null,
null);
}
public TreeNode(Object
anObject, TreeNode aLeftChild, TreeNode aRightChild) {
item = anObject;
rightChild = aRightChild;
leftChild = aLeftChild;
}
public final TreeNode rightChild() {
return
rightChild;
}
public final TreeNode leftChild() {
return leftChild;
}
public final void setRightChild(TreeNode child) {
rightChild = child;
}
public final void setLeftChild(TreeNode child) {
leftChild = child;
}
}
Notice that we called the class TreeNode. In fact,
every
node in the tree is a tree itself. It is actually a recursive
data
structure.
Here is an example of how to build the tree above:
public static void main(String
args[]) {
TreeNode root;
root = new TreeNode("A",
new TreeNode("B",
new TreeNode("D"),
new TreeNode("E",
new TreeNode("H"),
new TreeNode("I"))),
new TreeNode("C",
new TreeNode("F"),
new TreeNode("G",
new TreeNode("J"),
null)));
}
The height of a tree is the number
of nodes encountered along the longest path from (but not including)
the root to a leaf of the tree.
The tree above has a height of 3. Can you
write a recursive method that determines the height of a binary tree ?
public int height() {
if (leftChild == null)
if (rightChild
== null)
return
0;
else
return
(1 + rightChild.height());
else
if (rightChild
== null)
return
(1 + leftChild.height());
else
return
(1 + Math.max(leftChild.height(),
rightChild.height()));
}
| 5.7 Efficiency with
Recursion |
Although recursion is a powerful
problem solving tool, it has some drawbacks. A non-recursive (or
iterative) method may be more efficient than a recursive one
for two reasons:
- there is an overhead associated with large
number of method invocations
- some algorithms are inherently inefficient.
Example: Computing the nth Fibonacci
number can be written as:
| 1 |
if n = 0
|
| fib(n) = 1 |
if n = 1
|
| fib(n-1) + fib(n-2) |
if n > 1
|
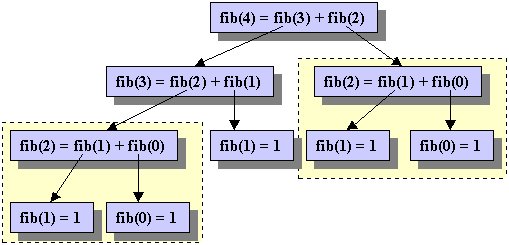
Notice in the above computation some problems
(e.g. fibonacci(2) ) are being solved more than once, even
though we presumably know the answer after doing it the first time.
The following iterative solution avoids this. (It
can also be
avoided with a properly formulated recursive solution)
public int finonacci(int n) {
if (n < 0)
return
-1;
int first = 1;
int second = 1;
int third = 1;
for (i=2;
i<=n; i++) {
third = first + second; //compute new value
first = second; second = third; //shift the
others
to the right
}
return third;
}
Try designing an efficient recursive Fibonacci method. You may
use indirect recursion.
Here are some points to remember about efficiency:
- Anything that can be done with a loop using
variables can be done recursively with the variables replaced by
parameters.
- In some languages like Lisp and Smalltalk,
recursion is normal. Consequently, recursive messages are implemented
very efficiently.
- In Lisp, for loops and while
loops are implemented recursively. Hence loops are no more (also
no less) expensive than recursive invocations.
Try writing recursive
methods for
the following problems:
Raising To
A Power
Consider the evaluation of xn,where
n is a non-negative integer.
- 1st Approach: (Could be done with
linear recursion)
- 2nd Approach (Recursive Formulation)
xn/2 * xn/2
if n is even
xn = x * xn-1
if n is odd
x0 =
1
if n is 0 (Basis Case)
Which approach would require fewer multiplications ?
Binary
Search:
Write a recursive method which would locate an
element in a sorted collection (i.e. Array or Vector) of n elements
without having to check all the elements
(as in the worst case). That is, we'd like the
maximum number of elements that need to be searched to be log(n).
The problem can be phrased recursively as follows.
- Basis Case: looking for an element in
a collection of size 1 is easy - just check the single element.
- Inductive Case: Look at the middle
element in the collection, if this bigger than the one you are looking
for
then search the portion of the collection before it. If it's
smaller
search the portion of the collection after it.
Notice how the problem of looking for an element in
a collection of size n, is phrased in terms of looking for an
element in a collection of size n/2. That's how we can be sure that only a logarithmic number
of elements need to be
examined.
A good exercise would be to build a SortedCollection
class from scratch and use a binary search to implement its contains(Object)
method (such as is implemented for class Vector).
The Tower
of Hanoi Problem
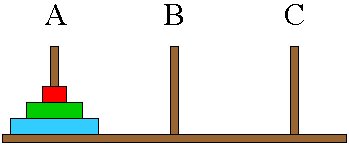
The task is to move the disks from peg A to peg B
using peg C as an intermediary (if necessary).
The rules are as follows:
- When a disk is moved, it must be placed on
one of the three pegs.
- Only one disk may be moved at a time, and it
must be the top disk on one of the pegs.
- A larger disk may never be placed on top
of a smaller one.
A solution is best understood by considering the
problem starting from simple cases to more complex cases.
Move (1 disk from A to B using
C) => JUST DO IT
Move (2 disks from A to B
using
C) =>
Move 1 A disk to C
Move 1 A disk to B
Move 1 C disk to B
Move (3 disks from A to B
using
C) =>
Move 2 A disks to C using B (use previous step)
Move 1 A disk to B
Move 2 C disk to B using A
...
Move (n disks from A to B
using
C) =>
Move n-1 A disks to C using B
Move 1 A disk to B
Move n-1 C disk to B using A
Implement a TowersOfHanoi application
which
will allow the user to specify some number of disks on one peg and then
select which other peg they should be moved to. The application
must them go
about moving the disks over following the rules above. This is a
good
application to animate on a graphical user interface.