Voronoi Diagrams and their properties

Nearest Neighbor Problem

The problem we want to address is called the Nearest Neighbor Problem: given a set of points $P$ and a point $p$, determine which point of $P$ is the nearest from $p$.

Figure 1: Delaunay Triangulation can not be directly used for the Nearest Neighbor Problem.

The first intuition we have is to use Delaunay Triangulation. Let $\mathcal{D}(P)$ be the Delaunay Triangulation of $P$, is it the case that the nearest point of $p$ is one of the three points incident to the face of $\mathcal{D}(P)$ containing $p$? Looking at Figure 1, we see that it may not be the case.

Figure 2: The bisectrix of two points.

Now, lets reduce the size of the problem to the case where $P$ contains only two points $p_1$ and $p_2$. In that case, the bisectrix of $p_1$ and $p_2$ divides the plane into two halves (see Figure 2), each of which containing the points respectively nearest to $p_1$ and $p_2$. This see this, first remember that the bisectrix is defined as the set of points which are equidistant from $p_1$ and $p_2$. Now, suppose that $p$ is on the same half-plane as $p_1$, and let $x$ be the intersection point between the bisectrix and the segment $\overline{pp_2}$. We have that:

$$d(p,p_2) = d(p,x) + d(x,p_2)$$ (1)

$$= d(p,x) + d(x,p_1)$$ (2)

$$\geq d(p,p_1)$$ (3)

where (2) comes from the definition of a bisectrix and (3) is the triangle inequality. We can then generalize this result to the case where we have more points. In that case, if we note $h(p_1,p_2)$ the half plane delimited by the bisectrix of $p_1$ and $p_2$ containing $p_1$, and $reg(p)$ the set of points nearest to $p$ than any other point of $P$, then we have:

$$reg(p) = \{q\vert d(p,q)\leq d(p_i,q)\forall p_i\in P (p_i\neq p)\}$$

$$reg(p) = \{q\vert q\in h(p,p_i)\forall p_i\in P(p_i\neq p) \}$$

$$reg(p) = \mathop{\bigcap}\limits_{p_i\in P(p_i\neq p)}h(p,p_i).$$

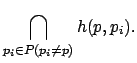This effectively form a partition of the plane, since (excepted points on the boundaries) every point is in exactly one region. Moreover, since the region of a point can be defined as the intersection of $n$ half-planes (where $n$ is the number of points in $P$), each of those regions can be computed, using linear programming, in $O(n\log n)$. Since we have $n$ such regions to compute, the whole set of those regions (which we shall call the Voronoi Diagram of $P$ and note $\mathcal{V}(P)$) can then be computed in $O(n^2\log n)$.

In the sequel, we will assume that no three points are collinear and no four points are cocircular.

Duality with Delaunay Triangulations

What we are now interested in is to improve the time needed to compute $\mathcal{V}(P)$. We will show that $\mathcal{V}(P)$ is the dual of $\mathcal{D}(P)$, and since computing the dual is an operation which can be done in linear time, and computing $\mathcal{D}(P)$ can be done in $O(n\log n)$ time, we will see that $\mathcal{V}(P)$ can be computed in $O(n\log n)$ time as well.

Figure 3: Delaunay is dual to Voronoi.

To see this, let $v$ be a vertex in $\mathcal{V}(P)$. That vertex is formed by the intersection of some bisectrix (at least two) and let $p_1$, $p_2$ and $p_3$ be some of the points used to define those bisectrix (there are at least three such points otherwise we would only have one bisectrix). This situation is illustrated on Figure 3. Then, we have that $v$ is equidistant from $p_1$, $p_2$ and $p_3$, meaning that $v$ is the center of the circle defined by $p_1$, $p_2$ and $p_3$. We claim that this circle contains no points of $P$. If that would be the case, then $v$ would be nearer from that point than from $p_1$, $p_2$ and $p_3$, and then would not be on the boundaries of $reg(p_1)$, $reg(p_2)$ and $reg(p_3)$. Therefore, in $\mathcal{D}(P)$, there is a Delaunay edge between $p_1$ and $p_2$, between $p_2$ and $p_3$, and between $p_3$ and $p_1$. Notice that $v$ may not ne in the triangle we just defined. We then showed that each edge in the dual of $\mathcal{V}(P)$ is a Delaunay edge. To see that each Delaunay edge is in the dual of $\mathcal{V}(P)$, similarly trace the unique circle defined by the three vertices $p_1$, $p_2$ and $p_3$ of a Delaunay face. That circle is empty, and its center is equidistant to each of the three vertices. We then have that this center is in $reg(p_1)\cap reg(p_2) \cap reg(p_3)$, meaning that $reg(p_1)$, $reg(p_2)$ and $reg(p_3)$ are touching, and therefore each Delaunay edge is in the dual of  $\mathcal{V}(P)$.

Counting Vertices and Edges

It is quite clear that for each $p\in P$, $p\in reg(p)$. Therefore, the number of faces in $\mathcal{V}(D)$ is equal to $n$, the number of points in $P$. Also, if we assume that no four points are cocircular, we have that each vertex is of degree 3, and then:

$$3V = \sum deg(v)$$

$$= 2E.$$

Now, Euler tells us that:

$$V - E + F = 2$$

$$V - \frac{3}{2}V + n = 2$$

$$V = 2n - 4.$$

Which allows us to deduce that:

$$E = 3n -6.$$

Unbounded Regions

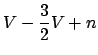The last property of Voronoi Diagrams we want to discuss is their relationship with Convex Hulls. We already know that $reg(p)$ is a convex region for each $p\in P$. Since $\mathcal{V}(P)$ form a partition of the plane, some points must have unbounded regions. We show that those points are exactly those lying on $CH(P)$.

Figure 4: The region of a point $p$ is unbounded if and only if $p$ is on the convex hull of $P$.

Let $p$ be a point that lies in $CH(P)$. Then, there is a line $l$ passing through $p$ such that all points of $P$ are on the same side of $P$. Let $h$ be the half-plane defined by $l$ not containing any point of $P$. Every point lying on the half-line perpendicular to $l$ and lying on $h$ has $p$ as its nearest neighbor, and then $reg(p)$ is unbounded.

Now, let $reg(p)$ be unbounded. This means that there is a half-line emanating from $p$ such that every point on that half-line has $p$ as its nearest neighbor. Let $l$ be the line perpendicular to that half-line and passing through $p$, and $h$ be the half-plane defined by $l$ on which the half-line lies. No point of $q\in P$ can be in $h$, otherwise, by going far enough on the half-line, we could find a point $r$ that is nearer to $q$ than $p$ (see Figure 4). Therefore, $p$ lies on $CH(P)$.