Skew Voronoi Diagrams

This section is a paper review of an article by Aichholzer, Aurenhammer, Chen, Lee and Papadopoulou entitled Skew Voronoi Diagrams (2). We put it here in order to give the reader an idea of how the Voronoi Diagram properties we saw in Section 1 can change if we use a distance function other than the euclidian distance.

Introduction

Given a set of points $S$, its associated Voronoi diagram is a partitioning of the plane $\mathcal{V}(S)$ into regions such that each region contains the points nearest to a particular point of $S$. For example, if $\vert S\vert=2$, then its associated Voronoi diagram is two half-planes separated by the bisectrix of the two points. In that definition, it is generally assumed that the word nearest refers to the smallest euclidian distance. However, in some applications, it may happen that the distance of interest is not the euclidian distance. As an example, consider the case where you are at the mountain and you have the choice between going ten steps upward and ten steps downward. Certainly, the ten steps you would make upward are more costly to you in terms of energy and time than the ten steps downward. In such cases, it appears that the euclidian distance does not tell you in which direction you should go. What we need is a distance function that takes into account the difference in height between two points. This is exactly what the skew distance, introduced in (2) does. In section 3.2, we will present the skew distance and some of its basic properties. In section 3.3, we take a look at the general shape of the Voronoi diagram under the skew distance. In section 3.4, we will discuss some computational issues about the Voronoi diagram under the skew distance. Finally, in section 3.5, we will show how it is possible to use some properties of the skew Voronoi diagram to design an efficient algorithm to solve the all nearest neighbors problem.

Skew Distance

The skew geometry takes place in a titled plane. For sake of simplicity, it considers that the $xy$ plane in $\mathbb{R}^3$ is rotated around the $x$ axis from an angle $\alpha$. Different angles of rotation give raise to different distances. If it is not rotated at all, then the distance you get is the euclidian distance. One simple way to define a distance function that reflects the fact that going up is harder than going down is to take the following function: $d(p,q)=d_2(p,q)+(z_q-z_p)$, where $d_2$ is the two dimensional euclidian distance and $z$ is the height of a point. Since $z_p$ = $y_p\sin(\alpha)$, one can then forget about the $z$ coordinates of its points, and say that the distance between two points is $d(p,q)=d_2(p,q)+\sin(\alpha)(y_q-y_p)$. Now, since $\sin(\alpha)$ is just a constant, we can generalize it to a family of distance functions $d(p,q)=d_2(p,q)+k(y_q-y_p)$. If we allow $k$ to take arbitrary positive values (greater than 1), we get an even richer set of distance functions.

Firstly, notice that the term distance here should not be understood under the traditional analytical meaning of the word. Usually, we expect a distance function $d$ to respect at least the four following properties:

1. having a range included in $\mathbb{R}^+$,
2. $d(x,y)=0\Rightarrow x=y$,
3. $d(x,y)=d(y,x)$ (symmetry),
4. $d(x,z)\leq d(x,y)+d(y,z)$ (triangle inequality).

The skew distance does not respect all those properties. As an example, take the case where $k=1.5$. If $q$ is vertically below $p$, then $d(q,p)<0$, meaning that $p$ is nearer to $q$ than $q$ itself. Also, $d(p,q)>0$, and the symmetry property is not respected. However, one can verify that the second is verified if $k<1$ and the fourth property is always respected.

Secondly, circles under skew distance have an interesting property: they are conics, and different values of $k$ leads to different conics. Remember that given a point $p$ and a radius $r$, the circle $c(p,r)$ is defined as $\{q\vert d(p,q)=r\}$. Since the skew distance is not symmetric, two different circles can be defined: the outgoing circle and the incoming circle. In the paper, the authors only look at the outgoing circle, saying that the incoming circle can be obtained by reflection. This are actually doing this for every geometric structure.

So lets take a look at outgoing circles under the skew distance. They satisfy the equation:

$$d(p,q) = r$$

$$d_2(p,q) + k(y_q-y_p) = r$$

$$\sqrt{\Delta x^2+\Delta y^2} + k\Delta y = r \mbox{ (with $\Delta x := x_q - x_p$\ and $\Delta y := y_q - y_p$)}$$

$$\sqrt{\Delta x^2+\Delta y^2} = r - k\Delta y$$

$$\Delta x^2+\Delta y^2 = (r - k\Delta y)^2$$

$$\Delta x^2+\Delta y^2 = r^2 - 2kr\Delta y + k^2\Delta y^2$$

$$\Delta x^2+ (1-k^2)\Delta y^2 + 2kr\Delta y = r^2$$

So if $k=0$, what we get is an euclidian circle, if $k=1$, we have a parabola, if $k<1$, we have an ellipse, and if $k>1$, we have an hyperbola. In particular, this means that it is possible to have unbounded circles.

Analyzing the Skew Voronoi Diagram

What we now want to do is to take a look at the general aspect of the Voronoi diagram of a set of points $S$ under the skew distance, which we shall denote by $SV(S)$. The questions we want to ask are the following:

1. what is the general shape of a border?
2. are all regions non-empty?
3. if not, which ones?

Once again, the value of $k$ determines the answer to those questions. If $k=0$, we have the euclidian Voronoi diagram. If $k<1$, then the skew distance is a convex distance. The authors do not pursue deeper the case $k<1$ because Voronoi diagrams under convex distance functions have already been studied in (4). The case $k>1$ is studied more attentively.

We first analyze the general shape of a border between two Voronoi regions. Remember that the definition of the Voronoi diagram allows to say that borders of two regions, say $reg(p)$ and $reg(q)$, lie on the bisectrix of points $p$ and $q$. That is, it satisfies the equation:

$$d(p,a) = d(q,a)$$

$$d_2(p,a) + k(y_a-y_p) = d_2(q,a) + k(y_a-y_q)$$

$$d_2(p,a) - d_2(q,a) = k(y_p-y_q)$$

Since the expression $k(y_p-y_q)$ does not depend on $a$, this means that borders are portions of hyperbolas. If $k=0$, the hyperbola degenerates to a strait line as expected. On Figure 6, we can see an animated gif taken from Oswin Aichholzer homepage (1) showing how changes the Skew Voronoi Diagram in function of $k$.

Figure 6: Skew Voronoi Diagram in Action.

Now, lets take a look at emptiness of regions. We noticed earlier that since the skew distance can take negative values, it is possible for a point to be farther from itself than from another point. Then, it might be possible point a point $p$ that $p\not\in reg(p)$. Now, if $p\in reg(q)$ then $d(q,p)<d(p,p)$, and by the triangle inequality, $d(q,a) < d(q,p) + d(p,a)$. Since $d(q,p)<0$, this leads to $d(q,a) < d(p,a)$ and therefore $a\not\in reg(p)$. In other words, $reg(p)=\emptyset$.

In the next section, we will discuss the problem of computing the skew Voronoi diagram. If we'd be able to know in a low cost fashion which regions are empty, then we could use this information to design a more efficient algorithm to compute the skew Voronoi diagram. In order to do this, the authors first introduce the notion of negative area of a point. The negative area of a point $p$, noted $N(p)$, is simply the set of points $q$ such that $d(p,q)<0$. The border $L_0(p)$ of that region can be characterized by the equation:

$$d(p,q) =$$ 0

$$d_2(p,q) + k(y_q-y_p) =$$ 0

$$\sqrt{\Delta x^2+\Delta y^2} = - k\Delta y$$

$$\Delta x^2+\Delta y^2 = k^2\Delta y^2$$

$$\Delta x^2+ (1-k^2) \Delta y^2 =$$ 0

$$\Delta x = \pm\sqrt{k^2-1} \Delta y$$

which means that the border is a half cone centered at $p$ and having absolute slope $\sqrt{k^2-1}$. Now, we define $N(S)$ as

$$N(S) := \mathop{\bigcup}\limits_{p\in S}N(p)$$

and $E_0(S)$ as the border of that region. Note that no $p\in S$ can be above $E_0(S)$ since $d(p,p)=0$. We already shown in the preceding paragraph that if $p$ is below $E_0(S)$ then $reg(p)=\emptyset$. Is the converse true? The converse is equivalent to $p\in E_0(S)\Rightarrow reg(p)\neq \emptyset$. But $p\in E_0(S)$ means that there is no $q\in S$ such that $d(q,p)<0$. In other words, there is no $q$ nearer to $p$ than $p$ itself. Therefore, $p\in reg(p)$. We thus proved the following result:

Proposition 1   If $k>1$, then $reg(p)\neq \emptyset$ if and only if $p\in E_0(S)$.

Computing the Skew Voronoi Diagram

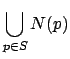We now take a look at the algorithmic issues concerning the skew Voronoi diagram. Obviously, we can not in general expect to able to compute it faster than the euclidian Voronoi diagram. Are there still cases where we can do better?

Firstly, are we able to use Proposition 1 to remove points from $S$ efficiently? By giving the plane an appropriate angle of rotation (which can be done in linear time), the authors show that the problem of finding which sites are below $E_0(S)$ can be reduced to the one of finding the maximal dominating elements of a set of points. Since that problem can be solved in $O(n\log h)$ time and $O(n)$ space (7), we can find which points have empty region with the same efficiency.

Secondly, once we have reduced our problem size, how efficiently can we compute the skew Voronoi diagram of the remaining? The authors show that the problem of computing the skew Voronoi diagram of a set of points can be reduced in linear time to the problem of computing the euclidian Voronoi diagram of a set of skew circles. In order to do this, first define $C(p)$ as the skew circle of center $p$ and radius $kp_y$. Then, notice that since between a point and a circle is the distance between that point and the center of the minus the radius the circle, we have:

$$d(p,a) = d(q,a)$$

$$d_2(p,a) - ky_p = d_2(q,a) - ky_q$$

$$d_2(C(p),a) = d_2(C(q),a)$$

which means that the skew bisectrix of two points $p$ and $q$ is equal to the euclidian bisectrix of the two circles $C(p)$ and $C(q)$. Using that information, the authors claim that it is simple to compute the euclidian Voronoi diagram of a set of circles by adapting the plane sweep algorithm that we have seen in Section 3.4. Since that algorithm runs in $O(n\log n)$ time and $O(n)$ space, they obtain the following result:

Proposition 2   It is possible to compute the skew Voronoi diagram in $O(n\log h)$ time and $O(n)$ space, where $h$ is the number of non-empty Voronoi regions.

All Nearest Neighbors Problem

The all nearest neighbor problem can be stated as follows: for each $p\in S$, find $q\in S$ such that $q\neq p$ and $d(q,p)$ is minimized. Note that, as opposed to the euclidian case, it is not necessarily the case that $q$ is a Voronoi neighbor of $p$. As an example, consider the case where $\vert E_0(S)\vert=1$ (that will be the case, for example, if $k>1$ and all points are vertically aligned). Then, let $p$ be the unique point in $E_0(S)$. Since $p$ has no Voronoi neighbor, it is straitforward that the nearest neighbor of $p$ is not a Voronoi neighbor of $p$.

Note also that once again, since the skew distance is not symmetric, there are two versions of the problem: the incoming version and the outgoing version. We will restrict our attention to the incoming version and note $neighto(p)$ the nearest incoming neighbor of $p$. Observe it is possible to use the fact that $p$ is in the Voronoi region of $neighto(p)$ in $SV(S\setminus\{p\})$ to develop an algorithm solving the problem in $O(n^2)$ time (once the points are sorted, each of the $n$ Voronoi diagrams takes $O(n)$ time to compute and finding the Voronoi region to which $p$ belongs takes $O(n)$ time).

The authors uses the fact that $neighto(p)$ is either is $E_0(S)$ or in $E_0(S\setminus E_0(S))$. This can be demonstrated by case analysis on wether $p$ is below $E_0(S)$ or not. If $p$ is below $E_0(S)$, then $neighto(p)$ is in $E_0(S)$ as we already shown. If $p$ is on $E_0(S)$, then $neighto(p)$ is on $E_0(S\{p\})$ which is a subset of $E_0(S\setminus E_0(S))$. We then have the following proposition:

Proposition 3   $neighto(p)\in E_0(S)\cup E_0(S\setminus E_0(S))$.

The algorithm we can derive using this fact goes as follows: Compute $SV(S)$ and $SV(S\setminus E_0(S))$. If $p$ is below $E_0(S)$, then do a planar point location in $SV(S)$. If it is not, then $neighto(p)$ is either the closest Voronoi neighbor of $p$ in $SV(S)$ or the point having the Voronoi region to which $p$ belongs in $SV(S\setminus E_0(S))$. Chose the closest one of those two points.

Since this algorithm requires to compute only two Voronoi diagrams, it can be performed in $O(n\log (h_1h_2))$ where $h_1$ is the number of Voronoi regions in $SV(S)$ and $h_2$ is the number of Voronoi regions in $SV(S\setminus E_0(S))$.